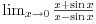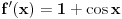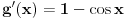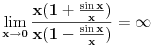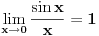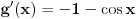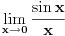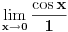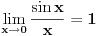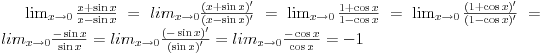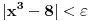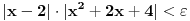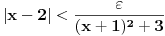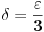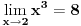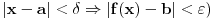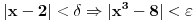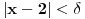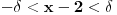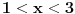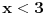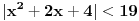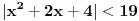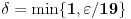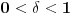Lopital može, nije -1. , , ne znam kako sada dobijaš -1. Inače bez izvoda:

, jer

1. Može Lopitalovo pravilo.
2. Ne nije -1. Pogledaj malo bolje šta ti je u brojiocu i imeniocu. |x| > |sin x| osim za x=0. pa su i brojilac i imenilac istog znaka.

Verovatno je bila greška u izvodu brojioca Umesto napisao je .

Btw, i se primenom Lopitalovog pravila svede na

Da, ali može i slabijim http://en.wikipedia.org/wiki/L...ction#Limits_of_extra_interest

Interesantno da i Wolframalpha to radi preko Lopitalovog pravila, ali su ga baš zakomplikovali...

Čisto da pomenem da se činjenica koristi u dokazu da je izvod sinusa kosinus, mada to zavisi i od izbora definicije sinusa.

Ovako sam dobio -1 . Ali nisam siguran, pa sam zato pitao. Ako je greska, a verovatno jeste, chim i na pomenutom WolframAlpha sajtu se dobije drugo resenje, zanima me gde je greshka pri ovakvom postupku.
Da li mozda u ovom koraku ne smem da koristim lopitala:


?

Uslov za primenu Lopitalovog pravila je da su limesi funkcija f(x) i g(x) ili nula ili beskonačno.

Posle prve primene pravila, dobijaš da su limes gornje funkcije 2, a donje 0, pa ne može više da se koristi.

Tačno.

Mene muci sledece: Kako dokazati ( po definiciji ) da je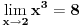

http://www.elitesecurity.org/t389338-0

Zamijeni dva umjesto iks-a.

Po definiciji je epsilon delta racun.

,



.

Za svakako iz sledi .

I niko da vidi grešku.

Za je , a samim tim i . Otuda za svakako iz sledi .

Zar nije ?

Da li je ispravno dokazati ovako:

Difinicija



E sad, moze li dokaz dalje ovako:


/+2

tj.
odakle sledi....

Na kraju,

Jel bi mi pomogao neko?

Prvo, otkud znaš da iz sledi . To je tačno za . Znači, moraš da napišeš taj uslov.

Drugo, sledi iz , što je kod tebe ispunjeno.

Dakle, treba da važi i . Drugim rečima, dovoljno je da bude .

Kad smo na casu vrsili takav dokaz, podrazumevali smo da je , jer kako kaze nas profesor, cilj je da bude sto manje. Tako da mi sami postavljamo uslov, pod kojim bi dokazali dati limes?