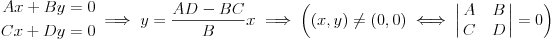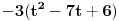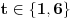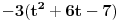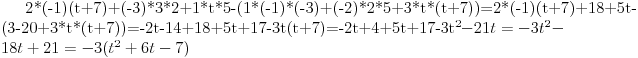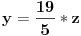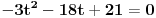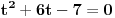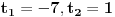[ different @ 06.09.2010. 14:53 ] @
Moze li mala pomoc,potrebno je odrediti parametar "t" ("t" je iz skupa realnih brojeva) tako da dati sistem ima netrivijalna rjesenja, a zatim rijesiti sistem. 2x+ty-3z=0 3x-y+5z=0 x-2y+(t+7)z=0 sistem znam kako rijesiti,ali kako da nadjem "t" uz navedeni uslov... |