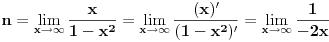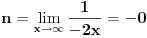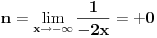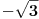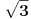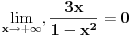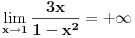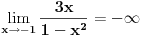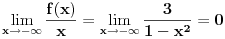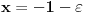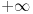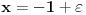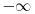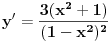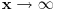[ lonelyrider_44 @ 09.09.2010. 01:59 ] @
Ovako, f-ja glasi: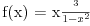 Prilikom ispitivanja, dobijem da f-ja ima kosu asimptotu ( 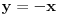 ), a ujedno ima i nulu f-je za x=0, a kroz tu tachku prolazi kosa asimptota! Pretpostavljam da je greshka u pitanju, samo ne mogu da je otkrijem. Chini mi se da prilikom trazenja kose asimptote postoji neshto zbog chega je nema, jer, chak i da je ima, imala bi smisla da glasi: ), a ujedno ima i nulu f-je za x=0, a kroz tu tachku prolazi kosa asimptota! Pretpostavljam da je greshka u pitanju, samo ne mogu da je otkrijem. Chini mi se da prilikom trazenja kose asimptote postoji neshto zbog chega je nema, jer, chak i da je ima, imala bi smisla da glasi: 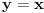 Kosa asimptota 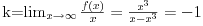 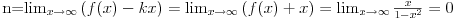 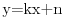  Za prvi izvod f-je dobio sam: 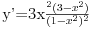 Drugi izvod: 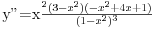 evo i slike:  Uploaded with ImageShack.us Unapred hvala na pomoci |