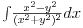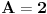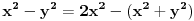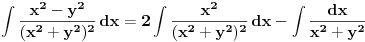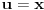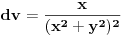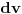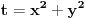Nisam sigurna, posto sam tek pocetnik u ucenju integrala, ali ja bih ovako pokusala:

I = ∫x^2dx/(x^2+y^2)^2 - ∫y^2dx(x^2+y^2)^2 =

= ∫(x^2+y^2-y^2)/(x^2+y^2)^2 dx – y^2 ∫dx/(x^2+y^2)^2 =

= ∫1/(x^2+y^2) dx – 2y^2 ∫1/(x^2+y^2)^2 dx =
= 1/y^2 ∫1/(1+(x/y)^2) dx – 2y^2 ∫y/cos^2 t * 1/(y^2tg^2 t+y^2)^2 dt =

= 1/y * arc tg x/y – 2y^2 ∫dt/(y^3 cos^2 t(sin^2 t/cos^2 t + 1)^2) =

= 1/y * arc tg x/y – 2/y ∫dt/(cos^2 t(1/cos^2 t)^2) =

= 1/y * arc tg x/y – 2/y ∫cos^2 t dt ;

Ovaj cu izracunati posebno:

∫cos^2 t dt = ½ ∫(1+cos 2t)dt = ½ ∫dt + ½ ∫cos 2t dt =

= ½ t + ¼ sin 2t + C = ½ arc tg(x/y) + ¼ sin(2 arc tg(x/y)) + C

I = 1/y * arc tg (x/y) – 2/y (½ arc tg(x/y) + ¼ sin(2 arc tg(x/y))) + C

I to se jos malo sredi...

Smene koje sam koristila:

smena 1: x = y * tg t
dx = y/cos^2 t dt
smena 2: x/y = z => dx = y * dz
smena 3: 2t = p => dt = ½ dp


P.S. Izvinjavam se ako nije tacno... :(

za i , odnosno za i . Dakle, , pa je



Prvi integral reši paracijalnom integracijom sa , (smena za je ), a drugi integral je tabličan.