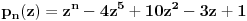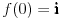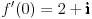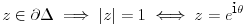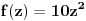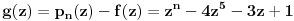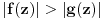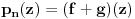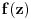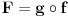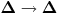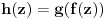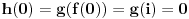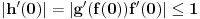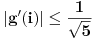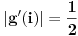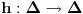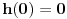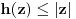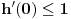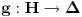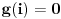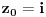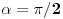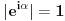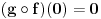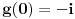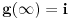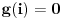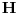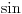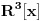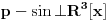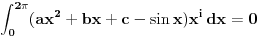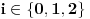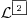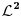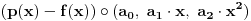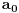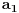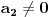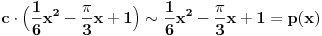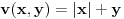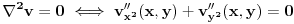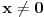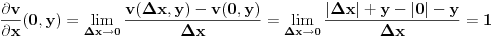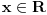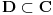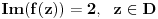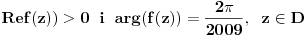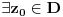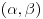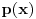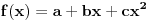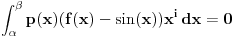[ Cabo @ 12.09.2010. 18:41 ] @
|
[ Goran Rakić @ 12.09.2010. 19:37 ] @
Funkcija g bi mogla da bude opšti oblik bilinearnog preslikavanja
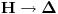 , , 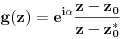 gde je gde je 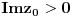 , a , a  proizvoljan ugao. proizvoljan ugao.Međutim kada izračunam 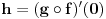 kao izvod složene funkcije ne znam šta dalje. Ako bi bilo kao izvod složene funkcije ne znam šta dalje. Ako bi bilo  po ŠL po ŠL 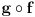 ne postoji, za ne postoji, za 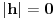 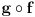 bi bila neka rotacija. Nejasno mi je i kako bismo zaključili da f ne postoji preko bi bila neka rotacija. Nejasno mi je i kako bismo zaključili da f ne postoji preko 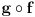 kada izaberemo neko g? kada izaberemo neko g?Ovo pod a) je u redu. Na granici važi 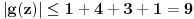 po nejednakosti trougla i iz po nejednakosti trougla i iz 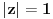 na na 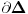 . . [Ovu poruku je menjao Goran Rakić dana 12.09.2010. u 20:51 GMT+1] [ Cabo @ 12.09.2010. 20:18 ] @
Hvala.
Pod b) sam zaboravio da mi je takođe rečeno da treba da se dobije, i dokaže, da ne postoji takva funkcija. Uzgred, moderatorima da poručim da mi baguje modem, pa sam zato nenamerno postavio temu više puta. Stalno dobijam "Connection was reset". [ Nedeljko @ 12.09.2010. 23:05 ] @
[ Goran Rakić @ 13.09.2010. 07:46 ] @
[ Nedeljko @ 13.09.2010. 09:15 ] @
Napisao sam kompletno rešenje. U čemu je problem?
[ Goran Rakić @ 13.09.2010. 09:16 ] @
Nema problema, rekao sam ti hvala. Usput upoređujem sa svojom prethodnom porukom i komentarišem gde sam napravio grešku u razumevanju.
[ Cabo @ 13.09.2010. 11:49 ] @
Pre svega, hvala Ti puno Nedeljko.
Citat: Nedeljko: 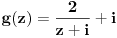 . .Znači, samo „lupim“ funkciju  ? Nema nekog posebnog postupka kako da se do nje dođe? ? Nema nekog posebnog postupka kako da se do nje dođe?A imam još jedan zadatak: U realnom Hilbertovom prostoru 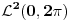 naći polinom drugog stepena, naći polinom drugog stepena, 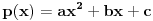 , koji je najbliži vektoru , koji je najbliži vektoru 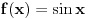 . Obrazložiti. . Obrazložiti.Rečeno mi je da treba da se posmatra rastojanje od projekcije (pretpostavljam vektora  ?) na potprostor (pretpostavljam ?) na potprostor (pretpostavljam 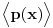 ?)“, i da „skalarni proizvod treba izjednačiti sa nulom“. ?)“, i da „skalarni proizvod treba izjednačiti sa nulom“.E, sad, da li to znači da se radi nešto ovako: 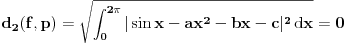 , ili nešto drugo? , ili nešto drugo?[ Nedeljko @ 13.09.2010. 12:20 ] @
[ Cabo @ 13.09.2010. 12:23 ] @
[ Nedeljko @ 13.09.2010. 12:26 ] @
[ Cabo @ 13.09.2010. 12:28 ] @
[ Nedeljko @ 13.09.2010. 12:29 ] @
Citat: Cabo: Odakle ovo sledi? Ma, ne sledi, ali moraš nekako da zadaš još dve tačke. Rub ide na rub, pa izaberi tačke sa ruba proizvoljno. Nekako se nameće inverzija kod koje će imaginarna osa da se slika u sebe. Na kraju moraš proveriti da je slika domena ono što treba. [ Nedeljko @ 13.09.2010. 12:31 ] @
[ Cabo @ 13.09.2010. 12:42 ] @
[ Nedeljko @ 13.09.2010. 12:48 ] @
Konjunkcija koju si napisao je dobra, ali to nije jedan skalarni proizvod, već su u pitanju tri skalarna proizvoda.
[ Cabo @ 13.09.2010. 13:09 ] @
[ Cabo @ 13.09.2010. 15:56 ] @
[ Nedeljko @ 13.09.2010. 16:12 ] @
Parcijalni izvod po x ne postoji na y-osi.
[ Cabo @ 13.09.2010. 16:25 ] @
[ Nedeljko @ 13.09.2010. 20:58 ] @
Da.
[ Cabo @ 14.09.2010. 09:17 ] @
[ epicentar @ 06.11.2010. 05:44 ] @
Moze li neko da mi, makar i okvirno, kaze kako se radi sledeci tip zadatka?
Ispitati (Lebeg) merljivost funkcije 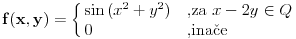 , a zatim odrediti , a zatim odrediti 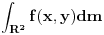 ,gde je m-Lebegova mera na ,gde je m-Lebegova mera na 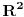 Ja "kao nesto" razmisljam ovako: AKO je skup 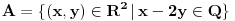 mere 0, onda je lako: mere 0, onda je lako:f=0 skoro svuda => f neprekidna skoro svuda => f merljiva Integral je, u tom slucaju 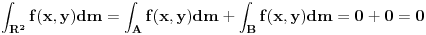 , gde je , gde je 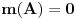 , , a na skupu 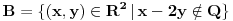 vazi vazi 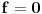 . .Sve je to lepo, "samo" ne znam da li je zaista 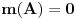 , i ako jeste, kako to da dokazem. , i ako jeste, kako to da dokazem. Dodatno se zbunjujem kod 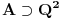 . .Ili sam, jednostavno, sve "promasila" ? Svaki odgovor je dobrodosao Hvala unapred! [ Nedeljko @ 06.11.2010. 13:59 ] @
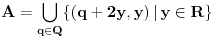 . Stoga je skup . Stoga je skup  mere nula kao prebrojiva unija skupova mere nula. Međutim, ovo nije tačno mere nula kao prebrojiva unija skupova mere nula. Međutim, ovo nije tačnoCitat: epicentar: f=0 skoro svuda => f neprekidna skoro svuda => f merljiva Karakteristična funkcija skupa racionalnih brojeva je jednaka nuli skoro svuda, ali je prekidna u svakoj tački. Međutim, neka je  merljiv skup predstavljen kao najviše prebrojiva disjunktna unija merljiv skup predstavljen kao najviše prebrojiva disjunktna unija 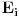 i neka su i neka su 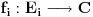 merljive funkcije. Tada je funkcija merljive funkcije. Tada je funkcija 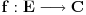 definisana kao definisana kao 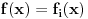 za za 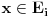 merljiva. Takođe, bilo kakva funkcija definisana na skupu mere nula je merljiva (i integrabilna sa integralom jednakim nuli) Pokušaj to da dokažeš i onda će ti ovo biti lako. merljiva. Takođe, bilo kakva funkcija definisana na skupu mere nula je merljiva (i integrabilna sa integralom jednakim nuli) Pokušaj to da dokažeš i onda će ti ovo biti lako.[ epicentar @ 06.11.2010. 14:19 ] @
Hvala, Nedeljko!
Javicu kad budem nesto uradila Drzite mi palceve :) Pozdrav! [ epicentar @ 06.11.2010. 16:43 ] @
Hmmm... Pa,sklepah nesto... Supljikavo...
1) Jasno mi je da je 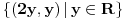 mere 0 (kao prava u mere 0 (kao prava u 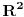 ), i da transliran za ), i da transliran za 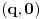 ne menja meru,dakle ne menja meru,dakle 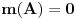 ,ali ne umem da formalizujem dokaz ,ali ne umem da formalizujem dokaz2) Zadrzavam sve pp-ke i oznake: 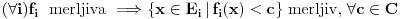 pa je 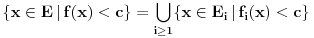 merljiv kao najvise prebrojiva (disjunktna) unija merljivih, pa je i sama f merljiva merljiv kao najvise prebrojiva (disjunktna) unija merljivih, pa je i sama f merljiva3) 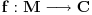 , gde je , gde je 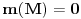 a f proizvoljna a f proizvoljna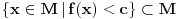 , pa je merljiv (mere nula), kao podkup skupa mere 0, dakle f je merljiva , pa je merljiv (mere nula), kao podkup skupa mere 0, dakle f je merljiva???? Sta fali? Uporno nesto propustam, ne izgleda mi ovo kako treba... Izvinjavam se na upornosti :) [ Nedeljko @ 06.11.2010. 17:58 ] @
[ epicentar @ 06.11.2010. 18:17 ] @
NEPROCENJIVO! :)))
Hvala jos jednom! P.S. Uputstvo je bilo,doslovce, savrseno [ Nedeljko @ 07.11.2010. 10:14 ] @
Prava je merljiv skup kao zatvoren skup, a karakteristična funkcija merljivog skupa je merljiva. Kada to znaš, onda meru skupa možeš odrediti kao integral karakteristične funkcije preko Fubinijeve teoreme.
[ epicentar @ 07.11.2010. 15:13 ] @
E, pa, tako Vam i treba kad zbunjujete zbunjenog!
Sad ne znam sta bih sa Fubinijem! Ovo, sledece? 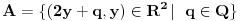 , kao i gore, pa je , kao i gore, pa je 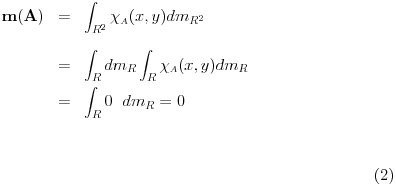 s tim sto je 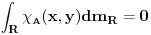 kao povrsina ispod kao povrsina ispod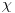 ,koje je jednostavna funkcija i uzima vrednost 1 na skupu mere 0 (samo kad je x=2y+q po 'x osi', za svako fixirano q po jednom, dakle na skupu mere m(Q)=0), i 0 inace. ,koje je jednostavna funkcija i uzima vrednost 1 na skupu mere 0 (samo kad je x=2y+q po 'x osi', za svako fixirano q po jednom, dakle na skupu mere m(Q)=0), i 0 inace.Smem da Fubinija ovako upotrebim? (posto ne mogu da izjednacim Rimana i Lebega jer mi f-ja nije neprekidna) [ Nedeljko @ 07.11.2010. 16:27 ] @
[ epicentar @ 07.11.2010. 21:11 ] @
Jedva protumacih...
Da, to sam otprilike i ja pokusavala da kazem ,samo u opisnom maniru, posto nisam umela bolje. I u mom zapisu je Vas 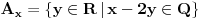 skup bio skup bio 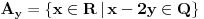 posto mi je 'unutrasnji' integral po x-osi. Sad je valjda OK. posto mi je 'unutrasnji' integral po x-osi. Sad je valjda OK.I moram da korigujem Vas prethodni post (greska pri kucanju), tek da nekom sledecem studentu olaksam... Citat: Nedeljko: Neka je 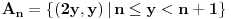 . Tada za svako . Tada za svako 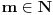 važi važi 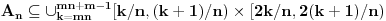 , odakle je , odakle je 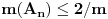 , odnosno , odnosno 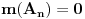 , pa je i , pa je i 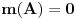 . Takođe, možeš na integral karakteristične funkcije skupa . Takođe, možeš na integral karakteristične funkcije skupa  da primeniš Fubinijevu teoremu. da primeniš Fubinijevu teoremu.Ovo ostalo ti je u redu. Treba: 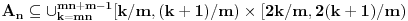 tj, imenilac je m tj, imenilac je mNe znam kako da Vam zahvalim za sve ovo; mozda izgleda kao jedan zadatak, ali sam mnogo stvari razjasnila zahvaljujuci ovoj prepisci. Hvala Vam jos jednom Pozdrav! [ epicentar @ 10.11.2010. 16:34 ] @
[ Nedeljko @ 10.11.2010. 22:23 ] @
Rešavaju se primenom Koši-Rimanovih uslova i to u Dekartovim koordinatama za prvi, odnosno polarnim za drugi zadatak.
[ epicentar @ 10.11.2010. 22:30 ] @
Hvala!
Stvarno mi to nije palo na pamet...ocekivala sam nesto komplikovanije :) [ Nedeljko @ 11.11.2010. 12:41 ] @
Postoji i opštiji pristup za rešavanje ovih problema.
Prvo, analitička funkcija čiji skup nula ima bar jednu tačku nagomilavanja u unutrašnjosti oblasti je konstantna u celoj oblasti. Iz toga i Tejlorove teoreme sledi da za ma koju nekonstantnu analitičku funkciju 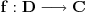 , gde je , gde je 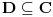 neka oblast i svaku unutrašnju tačku neka oblast i svaku unutrašnju tačku 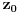 oblasti oblasti  postoje postoje  i analitička funkcija i analitička funkcija 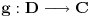 takvi da je takvi da je 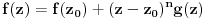 i i 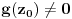 . Odatle sledi da slika bilo koje okoline tačke . Odatle sledi da slika bilo koje okoline tačke 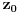 obuhvata sve tačke neke okoline tačke obuhvata sve tačke neke okoline tačke 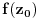 , odnosno da je slika otvorenog i povezanog skupa pri nekonstantnom analitičkom preslikavanju otvoren i povezan skup (povezanost sledi otuda što je slika povezanog skupa pri neprekidnom preslikavanju povezan skup). , odnosno da je slika otvorenog i povezanog skupa pri nekonstantnom analitičkom preslikavanju otvoren i povezan skup (povezanost sledi otuda što je slika povezanog skupa pri neprekidnom preslikavanju povezan skup).Zaista, najpre postoji analitička funkcija 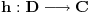 takva da je takva da je 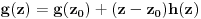 . Neka je dato . Neka je dato  takvo da takvo da 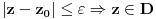 . Za neko . Za neko 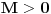 važi važi 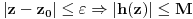 . Neka je . Neka je 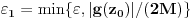 . Tada važi . Tada važi 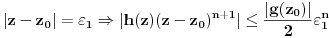 . Neka je . Neka je 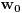 proizvoljan kompleksan broj takav da je proizvoljan kompleksan broj takav da je 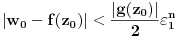 . Dokažimo da postoji . Dokažimo da postoji 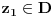 takvo da je takvo da je 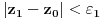 i i 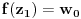 . .Zaista, 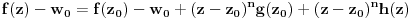 , kao i , kao i 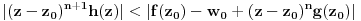 za za 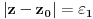 , pa je prema Rušeovoj teoremi dovoljno dokazati da je , pa je prema Rušeovoj teoremi dovoljno dokazati da je 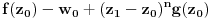 za neko za neko 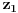 za koje je za koje je 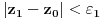 . Ta jednačina je ekvivalentna sa . Ta jednačina je ekvivalentna sa 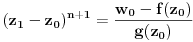 . No, traženo rešenje postoji zbog . No, traženo rešenje postoji zbog 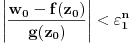 . .[Ovu poruku je menjao Nedeljko dana 11.11.2010. u 19:18 GMT+1] [ epicentar @ 12.11.2010. 05:58 ] @
Jasni su mi koraci, ali ne znam da li dobro sagledavam poentu...
Primenjeno na gore navedene zadatke: 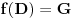 gde je G prakticno interval na pravoj (uz pretpostavku gde je G prakticno interval na pravoj (uz pretpostavku 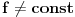 ) )Ako posmatram 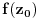 proizvoljno blisko granici oblasti G, uvek mogu da nadjem proizvoljno blisko granici oblasti G, uvek mogu da nadjem 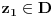 koje se slika u okolinu tacke koje se slika u okolinu tacke 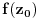 , sto, s obzirom na 'prirodu' oblasti G upravo znaci da postoji , sto, s obzirom na 'prirodu' oblasti G upravo znaci da postoji 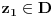 za koje za koje 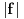 dostize minimalnu vrednost ? dostize minimalnu vrednost ? P.S. Sutra polazem pismeni, za par dana cu Vam javiti kako smo prosli na istom :) [ Nedeljko @ 12.11.2010. 07:09 ] @
Ma, slika otvorenog skupa je otvoren skup. D je otvoren, G nije otvoren, gotovo. Takodje, svaka unutrašnja tačka od D se mora slikati u unutrašnju tačku od G. Nema veze sa principom minimuma/maksimuma modula, već sa principom očuvanja oblasti.
[ epicentar @ 12.11.2010. 07:17 ] @
Pa tako mi kazite! Ja se uhvatila za minimum kao pijan plota, i ne vidim dalje od toga...
[ Dijana1986 @ 07.02.2013. 08:56 ] @
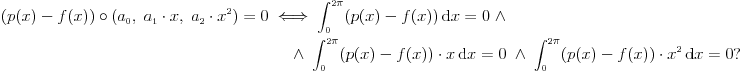 Da li mi neko može reći , kako iz ovih uslova da nađem koeficijente a,b i c tako da dati polinom bude drugog stepena. Rešavajući ova tri integrala dobijam tri jednačine sa tri promenljive ali dobijem da je koefcijent a jednak nuli, što nije dobro. Da li je dobra postavka ovih integrala? Inače zadatak glasi : Naći polinom drugog stepena koji je najbliži vektoru sinx u realnom Hilbertovom prostoru [ Nedeljko @ 07.02.2013. 10:07 ] @
[ Dijana1986 @ 07.02.2013. 11:31 ] @
Kada rešim integrale , dobijem tri jednačine sa tri nepoznate (a,b,c) i dobijem da je a = 0 , a to onda nije polinom drugog stepena.
Rečeno je da je p(x) polinom drugog stepena koji je najbliži vektoru sinx u realnom Hilbertovom prostoru. [ Dijana1986 @ 07.02.2013. 11:49 ] @
Interval je od 0 do Pi i tu je težinska funkcija P(x)=1, što znači da je podintegralna funkcija razlika polinoma drugog stepena i vektora sinx ali non stop dobijam da je a=0.
[ Nedeljko @ 07.02.2013. 14:47 ] @
U zadatku je trebalo da piše "stepena ne većeg od drugog". Standardno sam nailazio na tu nepreciznost u izražavanju.
[ Dijana1986 @ 07.02.2013. 14:57 ] @
Da li to znači , da i onda uzima vrednosti 0 i 1.
Meni je ovo zadatak sa ispita , konsultovala sam se sa jednim profesorom on kaže da može da a bude jednako nula i da je to opet polinom drugog stepena. [ Nedeljko @ 08.02.2013. 01:14 ] @
Ako je a=1, onda je polinom svakako drugog stepena. No, ako je a=0, onda je polinom stepena manjeg od dva. To je zapravo nepreciznost koja se provlači kroz mnoge knjige. Umesto "najviše drugog stepena" napišu "drugog stepena".
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|