Dobro si uzela. U čemu je problem?

rijeseje je x=0 ali meni ne moze da izadje tako..

Pa, napiši postupak, da vidimo gde si pogrešila. Jasno je da je x=0 jedno od rešenja, jer su obe strane jednake nuli.

za dv=t/(1+t^2)
v=inegral t/(1+t^2)
i kad rijesavam taj integral na kraju imam
v=1/2*itegral dz/korijen od z
e sad me interesuje hocu li uzeti ln IzI ili 2*korije od z

Pogledaj sajt: matematiranje.com . Tamo cesh naci uputstva za reshavanje integrala, konkretno shta uzimati za u i dv kod parcijalne integracije.

Izvinjavam se ako neko bude mislio da je u pitanju reklama. Samo preporuchujem jer mislim da moze da koristi.

Za integrale je po mom mišljenju najbolja zbirka Borisa Apsena. On je vrlo pregledno klasifikovao razne vrste integrala i načine kako se rešavaju.

hvala ti za taj sajt...rijesila sam zadtaka..

Po mom mišljenju, od Apsena treba bežati ko đavo od krsta. Jako loša knjiga iz koje se stiče utisak kao da si nešto razumeo, a kad ti neko zada elementaran zadatak koji zahteva samo razumevanje pojmova, sledi jedno veliko muuu.

Ja iz njega naučih kako da rešavam integrale racionalnih funkcija. :-/ Pre toga nisam imao blage veze sa tim.

Ama, dobro, svako je rekao svoje mišljenje.

kako d auradim ovaj integral koju smjenu da uzmem

integral (korijen od (1+t^2)) / (1+t^2)=

.

Uzmi jednu od smena

,

,

.

Sve tri pale.

Tabličan integral.
Rešenje mu je ln(t + koren(t^2+1)).

Tako je najbrže, a može i smenom.

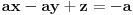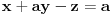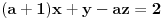ovde ne mogu da resim kad je (a+1)=0, sve sam probao....ako moze pomoc, i oko ovog!!!!
Odrediti supremum,infimum,maksimum i minimum... x pripada R a skup A= http://www.wolframalpha.com/in...%5Clog%5B4%2Cx%5E2-6%5D%5D%3E0 , ovde ne znam da l' gresim infimum je 0 i nema minimuma... Al sad za supremum razmisljam da bi najveca vrednost bila kad bi http://www.wolframalpha.com/input/?i=log%5B4%2Cx%5E2-6%5D%5D%3E0 bila veoma blizu 0, sto ispada da supremum ne postoji( posto bi za veoma malo iznad nula sama vrednost tezila beskonacno).....

Za sistem se svodi na


.

Iz druge jednačine je , dok zbir te dve jadnačine daje . Sistem dakle ima beskonačno mnogo rešenja.