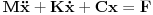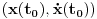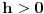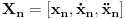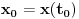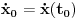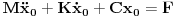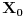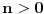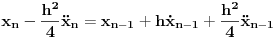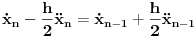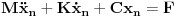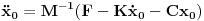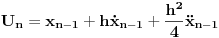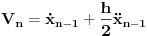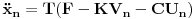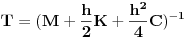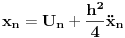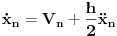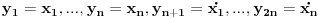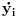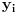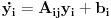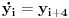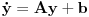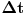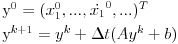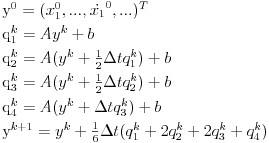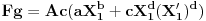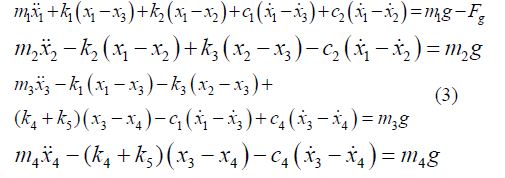|
|
[ zaricmica @ 16.09.2010. 12:11 ] @
|
| E ovako. Radim na jednom programu. Tacnije to mi je seminarski iz Bioinzenjeringa. Zadatak je da se na osnovu doskocne sile izracunaju neki koeficijenti u zglobu,. kolenu i kuku. E sad da bi se pocelo sa tim, treba da se resi sistem jednacina oblika Mx'' + Kx' + cX=F. Ima 4 jednacine sa X1,X2,X3 i X4. I i sa izvodima ovih promenljivih. Kod treba da napisem u C# sto mi nije problem, ali mi je problem kako da resim ovaj sistem. Kojom metodom. Ako neko moze da mi pokaze, bio bih veoma zahvalan. Napominjem da nemam pojma o dif jednacinama, tacnije o numerickim metodama resavanja.
|
[ Nedeljko @ 16.09.2010. 14:07 ] @
Čekaj, ako ti je to seminarski, trebalo bi da ste to učili ili da si dobio literaturu.
[ zaricmica @ 16.09.2010. 14:39 ] @
Ma nista nisam dobio :)
[ Nedeljko @ 16.09.2010. 14:53 ] @
A šta ste učili na datu temu? Jesi li se obratio profesoru?
[ miki069 @ 16.09.2010. 15:20 ] @
Šta su M, K, C i F: konstante ili funkcije?
Pravi sistem ili svako od X1 do X4 ima svoju diferencijalnu jednačinu?
[ p3j4 @ 16.09.2010. 17:55 ] @
Secam se iz dinamike konstrukcija ucili smo jedan deo o nelinearnoj analizi gde se diferencijalna jednacina dinamicke ravnoteze resavala numerickom integracijom preko Newmarkovog metoda. Proguglaj to pa vidi, mozda ti bude od pomoci...
[ zaricmica @ 16.09.2010. 22:02 ] @
Meni je profesor rekao da uradim Newmarkovom metodom. Nalazio sam nesto, ali mi je nejasno, posto nismo radili numericke metode. Mi smo radili samo osnovne tipove diferencijalnih jednacina. Koje smo resavali integraljenjem. Sad je ovo nesto novo za mene. A, M,C,K i F su konstante.
[ miki069 @ 16.09.2010. 22:10 ] @
Pravi sistem (u svakoj jednačini se pojavljuje više nepoznatih funkcija X1 do X4)
ili svaka nepoznata funkcija od X1 do X4 ima svoju diferencijalnu jednačinu?
Napiši primer sistema.
[ zaricmica @ 16.09.2010. 22:33 ] @
7X1"+6000(X1-X3)+5000(X1-X2)+250(X1'-X3')+600(X1'-X2')=68,67 - Fg
gde je Fg poznata vrednost nego nisam racunao.
6X2"-5000(X1-X3)+9000(X2-X3)-600(X1'-X2')=58,86
14X3"+6000(X1-X3)+9000(X2-X3)+25000(X3-X4)+250(X1'-X3')+1700(X3'-X4')=137,34
45X4"-25000(X3-X4)-1700(X3'-X4')=441,45
To je sistem :) "-drugi izvod, '-prvi izvod.
[ Nedeljko @ 17.09.2010. 13:51 ] @
Ako je to ovaj metod, ja sam ga razumeo ovako:
Dati su jednačina 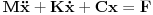 , početni uslov 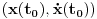 i korak 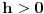
Formira se niz 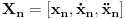 na sledeći način:
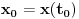 , 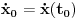 , 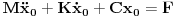 . Tako nalazimo 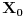 .
Za 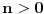 je
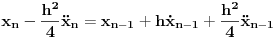 ,
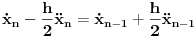 ,
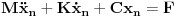 .
Rekapitulacija:
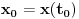 , 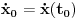 , 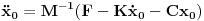 ,
Za 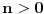 :
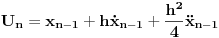 , 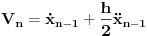 ,
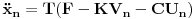 , za 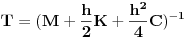 (primetiti da je  konstantno),
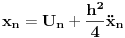 ,
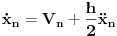 . [ Časlav Ilić @ 17.09.2010. 14:09 ] @
Prvi korak je da transformišeš sistem tako da ima samo prve izvode, uvođenjem smene 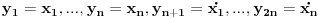 . Zatim na levoj strani ostaviš samo prve izvode 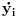 , a ostalo prebaciš na desnu i izdvojiš koeficijente uz 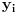 . Tada desnu stranu možeš da izraziš kao proizvod matrice poznatih koeficijenata i vektora 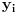 , pa sabrano sa još jednim poznatim vektorom, tako da ispadne 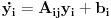 . Na to se dodaju jednačine usled smena 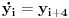 , pa još ako odbacimo indekse, ispadne matrična jednačina 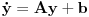 . Sada možeš da upotrebiš bilo koju metodu za numeričko rešavanje ovakvog sistema, najjednostavnije Ojlerovu, ili mnogo tačniju Runge-Kutinu četvrtog reda. (Ove dve su najpopularnije, a Njumarkova je koliko vidim negde između po složenosti i tačnosti, ne znam da li ima neku prednost u ovom kontekstu.) Ako je  indeks vremenskog trenutka, a 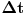 vremenski korak, Ojlerova metoda primenjena na ovaj sistem glasila bi:
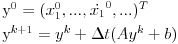
a Runge-Kutina četvrtog reda:
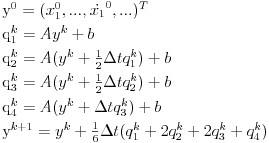
Ovako bi to izgledalo u pitonu (možda sam dobro presložio koeficijente, a možda i nisam), za nulte početne uslove i nulto 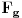 :
Code:
# -*- coding: UTF-8 -*-
from numpy import matrix
# Sistem ODJ prvog reda y' = A y + b.
A = matrix([
[0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 1],
[(-6000 -5000)/7.0, (+5000)/7.0, (+6000)/7.0, 0, (-250 -600)/7.0, (+600)/7.0, (+250)/7.0, 0],
[(+5000)/6.0, (-9000)/6.0, (-5000 +9000)/6.0, 0, (+600)/6.0, (-600)/6.0, 0, 0],
[(-6000)/14.0, (-9000)/14.0, (+6000 +9000 -25000)/14.0, (+25000)/14.0, (-250)/14.0, 0, (+250 -1700)/14.0, (+1700)/14.0],
[0, 0, (+25000)/45.0, (-25000)/45.0, 0, 0, (+1700)/45.0, (-1700)/45.0],
])
Fg = 0.0
b = matrix([
0.0,
0.0,
0.0,
0.0,
(+68.67 -Fg)/7.0,
(+58.86)/6.0,
(+137.34)/14.0,
(+441.45)/45.0,
]).transpose()
# Početni uslovi.
y0 = matrix([
# Početni položaji: x_1|0, ..., x_4|0.
0.0,
0.0,
0.0,
0.0,
# Početne brzine: x_1'|0, ..., x_4'|0.
0.0,
0.0,
0.0,
0.0,
]).transpose()
# Parametri integracije.
end_time = 1.0
num_steps = 100
dt = end_time / num_steps
print u"Krajnje vreme: %g" % end_time
print u"Broj koraka: %d" % num_steps
print u"Korak: %g" % dt
# Ojlerova metoda.
print u"Integralim..."
y_eu = y0
for k in range(num_steps):
y_eu = y_eu + dt * (A * y_eu + b)
print u"Konačni položaji i brzine Ojlerovom metodom:"
print y_eu
# Runge-Kutina metoda četvrtog reda (R-K 4).
print u"Integralim..."
y_rk4 = y0
for k in range(num_steps):
q1 = A * y_rk4 + b
q2 = A * (y_rk4 + 0.5 * dt * q1) + b
q3 = A * (y_rk4 + 0.5 * dt * q2) + b
q4 = A * (y_rk4 + dt * q3) + b
y_rk4 = y_rk4 + (1.0 / 6) * dt * (q1 + 2 * q2 + 2 * q3 + q4)
print u"Konačni položaji i brzine metodom R-K 4:"
print y_rk4
Ako se korak integracije smanjuje (tj. povećava krajnje vreme ili smanjuje broj koraka), rezultat će očekivano polako gubiti na tačnosti, ali će takođe pri određenom prevelikom koraku potpuno „odlepiti“ (izvršiti program za brojeve koraka npr. 50 i 60). To je tzv. granica stabilnosti za eksplicitne metode (kakve su i Ojlerova i R-K 4), i zavisi od jednačine koja se rešava.
[ zaricmica @ 17.09.2010. 15:44 ] @
Ja se izvinjavam. Doslo je do greske. Fg nije numericka vrednost. Vec je data formulom Fg= Ac(a*X1^b+c*X1^d*X1'^e)
^-na stepen
a= 1X10^6;b=1.56;c=2X10^4;d=0.73;e 1.0.
Izvinjavam se, ali mi je ovo hitno posto idem u nemacku za nedelju do dve, pa moram da zavrsim ispit. Ako mozete da pustite kroz program, da vidim koja su resenja. Hvala vam puno i bez toga.
[ Nedeljko @ 17.09.2010. 16:29 ] @
Časlave, rečeno joj je kojom metodom da radi. Ne trebaju joj ni Ojlerova metoda, ni metoda Runge-Kuta.
[ Nedeljko @ 17.09.2010. 16:30 ] @
@zaricmica
Već sam ti raspisao algoritam. Šta sad nije u redu? Ako nešto nisi razumela ili ti još nešto zapinje, reci.
[ zaricmica @ 17.09.2010. 16:33 ] @
Nije bitna metoda. Bitno mi je samo da dobijem resenja za X1,2,3,4. Kojom metodom nebitno. Mogu i u matlab da pustim da resi sistem. Ali ne znam kako.
[ Nedeljko @ 17.09.2010. 16:43 ] @
Onda ti je Časlavov predlog najjednostavniji.
[ atomant @ 17.09.2010. 19:43 ] @
Mogu ja u Matlabu da ti napisem ta 3-4 reda koja ce ti resiti ovo (mislim da koristi RK4), ali prvo mi objasni sta je ovo?
Fg= Ac(a*X1^b+c*X1^d*X1'^e). Sta je Ac? Za Fg sam video da figurise u jednacini, koeficijente si dala. Zanima me samo sta je Ac?
[ zaricmica @ 17.09.2010. 20:02 ] @
Ac=2.0 izvinjavam se sto nije stavljeno...
[ Nedeljko @ 18.09.2010. 00:57 ] @
Prilažem C++ program, doduše netestiran, pa probaj sa njim. Može se kompajlirati bilo kojim C++ prevodiocem. Preporučujem da skineš Code::Blocks sa MinGW prevodiocem.
Na početku treba da uneseš početnu i krajnju vrednost za t, korak i početni uslov. Ja nisam mogao da ih unesem u program, jer nisu zadati.
Malo mi je sumnjiv tvoj izraz za 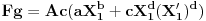 . Proveri da li si ga dobro prepisao. [ zaricmica @ 18.09.2010. 09:06 ] @
Tacan je izraz. Posto je Fg vertikalna kontaktna sila i zavisi od koeficijenata a,b,c,d,e i X1.
[ zaricmica @ 18.09.2010. 13:48 ] @
@Nedeljko, ovo mi je bilo od velike pomoci. Mislim hvala svima. Meni bi najvise odgovaralo da uradim u okviru programa koji pravim. A radim u c#. Mogu i gotove vrednosti da unesem, ali bi valjalo da program racuna, jer moze doci do promene ovih koeficijenata. Vec ste mi dosta pomogli. @Nedeljko ako znas malo c#, pravi mi problem, ne mogu da definisem moj tip podataka, kao ni referencu. Na netu mi nisu od pomoci konvertori.
[ Nedeljko @ 18.09.2010. 17:05 ] @
Ti reče da pisanje na C# jeziku nije problem. Sve što treba je da razumeš onaj program i napišeš svoj po ugledu na njega. Ne mora biti isti.
[ zaricmica @ 18.09.2010. 17:17 ] @
Ma ok je to. Lako cu ja analogno tome da napisem. Nego mi pravi neke greske. Npr. logaritam kod Fg. Posto se trazi log(arg[0][0]) pa to na b, pa mi tu brka nesto oko tipova promenljivih.
Double Fg = Ac * ((a * Math.Pow(Math.Log(arg[0,0]),b) ) + c * arg[0, 0] ^ d * arg[0, 1] ^ e1); ovo je deo koda. I izbaci mi ovu gresku
Error 1 Operator '^' cannot be applied to operands of type 'double' and 'double' E:\fax\bioinzenjering\master\Proba1\Proba1\Form1.cs 42 31 Proba1
[ pajaja @ 18.09.2010. 18:01 ] @
^ je logicki XOR operator a tebi koliko sam razumeo tu treba stepen.
[ zaricmica @ 18.09.2010. 18:54 ] @
Pa da. To i mene buni. Ne znam odakle to sad, posto sam digao na stepen.
[ zaricmica @ 18.09.2010. 18:56 ] @
Pa da. To i mene buni. Ne znam odakle to sad, posto sam digao na stepen.
[ Nedeljko @ 18.09.2010. 20:25 ] @
Ne, nisi. To što si napisao je XOR. Stepenovanje je Pow.
[ zaricmica @ 19.09.2010. 22:12 ] @
Pa ja sam stavio Math.pow()i izraz u zagradi. Ali snasao sam se :D uradio sam for naredbu :) hvala svima na ovolikoj pomoci. Pomogli ste mi stvarno mnogo
[ Nedeljko @ 20.09.2010. 09:49 ] @
Citat: zaricmica: Ma ok je to. Lako cu ja analogno tome da napisem. Nego mi pravi neke greske. Npr. logaritam kod Fg. Posto se trazi log(arg[0][0]) pa to na b, pa mi tu brka nesto oko tipova promenljivih.
Double Fg = Ac * ((a * Math.Pow(Math.Log(arg[0,0]),b) ) + c * arg[0, 0] ^ d * arg[0, 1] ^ e1); ovo je deo koda. I izbaci mi ovu gresku
Error1Operator '^' cannot be applied to operands of type 'double' and 'double'E:\fax\bioinzenjering\master\Proba1\Proba1\Form1.cs4231Proba1
Crvenim sam ti označio mesta gde si upotrebio XOR operator umesto stepenovanja. Svuda moraš da koristiš Math.Pow(). To sa for petljom neće funkcionisati za izložioce koji nisu celi. [ zaricmica @ 21.09.2010. 13:08 ] @
@Nedeljko
Jaoo jeste, nisam promenio ceo red. Ali i pored toga mi nalazi mnogo gresaka. Kad se mnozi h*(k[j]) prijavljuje neke gluposti i slicno. Jel mogu ja da povezem nekako onaj c program sa c#, posto bi trebao da imam interfejs. Ja sam izmenio da se unose neki koeficijenti koje sam zamenio u jednacinu, i to radi super. E sad mi treba da to nekako povezem sa c# zbog dijaloga.
[ Nedeljko @ 21.09.2010. 13:31 ] @
Pa, i u jeziku C++ se mogu praviti dijalozi. No, pustimo sad to. Okači taj tvoj C# program i napiši šta izbacuje, pa da vidimo. Sasvim je moguće da si zaboravio tačku-zarez ili neku sličnu glupost.
[ zaricmica @ 21.09.2010. 14:39 ] @
Evo saljem. Nisam ni zavrsio sve sto se tice kucanja. Odustao sam kad sam video koliko ima gresaka :D
[ Nedeljko @ 21.09.2010. 17:18 ] @
Probaj sa ovim. Za prevođenje će ti trebati Qt SDK (LGPL izdanje). Možeš ga naći na adresi
http://qt.nokia.com/downloads
Otvori .pro fajl u Qt Creatoru i pritisni Ctrl-R. [ Nedeljko @ 21.09.2010. 18:30 ] @
Ja i dalje mislim da si nešto debelo zeznuo u jednačinama.
[ zaricmica @ 21.09.2010. 18:56 ] @
Nisam. Tebe sigurno buni ono Fg. Poenta ovoga je da se nadje to Fg. Sila doskoka. Pa da vidim da li odgovara rezultatima dobijenim merenjem. Ono su samo jednacine dobijene od profesora, koje mi je dao sa koeficijentima, koje sam ja zamenio u jednacinama. Mada bolje da nisam menjao, posto mi je sad rekao da mu napravim za unos tih koeficijenata. Pa sam zbog toga u startu pokusao u c#, posto mi je laksi zbog formi. A ocekivao sam da ce mi traziti tako nesto.
[ Nedeljko @ 22.09.2010. 01:01 ] @
Evo ti ispravljene verzije, koja izbacuje i Fg.
[ zaricmica @ 22.09.2010. 10:40 ] @
@Nedeljko, atachovao sam prepravljen program. Tacnije prepravio sam funkciju. Izbacio sam vrednosti, a ubacio koeficijente. Mislim promenljive koje treba da se unesu. k1,k2,k3,k4,k5,m1,m2,m3,m4,c1,c2,c4. To mi je trazio profesor, da mi bude fleksibilnije. Ja sam ubacio to u deo koda za racunanje der. Ako mozes da mi povezes to sa formom, posto ja ne mogu da se snadjem u onome. Hvala i na ovome puno.
[ zaricmica @ 23.09.2010. 14:57 ] @
@Nedeljko, ja sam prepravio ovo, kako meni treba. Vidi da li je to sve u redu, mada mislim da jeste. Hvala i pozdrav.
[ TRAJKO41 @ 30.09.2011. 20:12 ] @
Imam slican problem u vezi resavanja jednacina. Naime, u mom slucaju sila Fg je pocetni uslov tj imam vrednosti za silu Fg za 1000 koraka tacnije za vremenski interval od 0 do 10s. Znaci za silu Fg ne koristim onu formulu koja je data. Treba da izracunam X1, X2, X3, X4 kao i prve i druge izvode i njih da prikazem kao grafik X1-t, X1'-t i X1''-t. Mogu li ja za ovaj problem da koristim ovu metodu ili ne? Slabo stojim sa diferencijalnim jednacinama.
[ Nedeljko @ 30.09.2011. 21:37 ] @
Moraćeš prvo precizno da opišeš problem, pa da postaviš jednačinu.
[ zaricmica @ 30.09.2011. 21:54 ] @
Trajko je bio moj cimer, i dobio je istu temu. Naime, jednacine su skroz iste, samo sto on sad mora da unese Fg kao pocetni uslov, a da dobije x1 kao rezultat. Kod mene je bilo obrnuto, ja sam morao da dobijem Fg.
Pozdrav,
Milutin.
[ TRAJKO41 @ 30.09.2011. 22:41 ] @
Ovo su jednacine
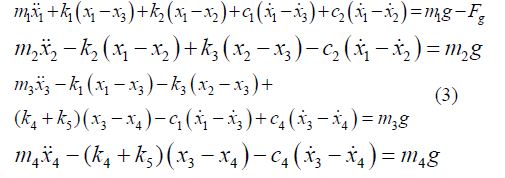
Sila Fg je zadata ovako file:///C:/Users/Danijel/Desktop/sila%20Fg.txt
Profesor mi je rekao da mi je to pocetni uslov i da treba da izracunam:
1. pomeranja tj vrednosti od X1 do X4
2. brzine tj X1' do X4'
3. Ubrzanja yj X1'' do X4''
I da nacrtam grafike za svaki od ova tri dela.
Nije mi jasno kako da ubacim silu Fg kao pocetni uslov.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|