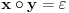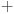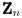[ grancica @ 18.09.2010. 21:45 ] @
| Napisati sve elemente prstena Z13 ostataka po modulu 13, a zatim za svaki od njih odrediti njegov inverz (ako postoji) u odnosu na operacije sabiranja i mnozenja po modulu 13. Da li je Z13 polje. Obrazlozi odgovor. Ono sta se moglo uraditi po mojim mogucnostima: Z13 ne znam koje brojeve sadrzi. PS. Ovaj zadatak ne mogu ni poceti, nadam se da necete brisati ovu poruku :) [Ovu poruku je menjao grancica dana 18.09.2010. u 23:54 GMT+1] |