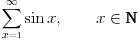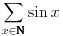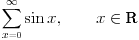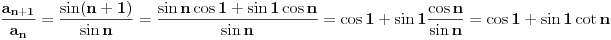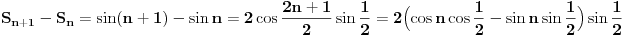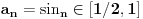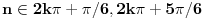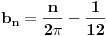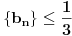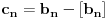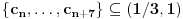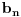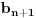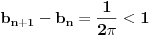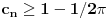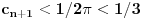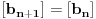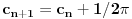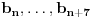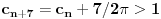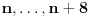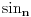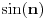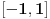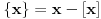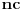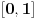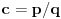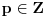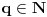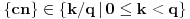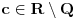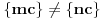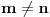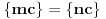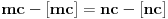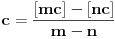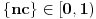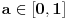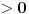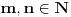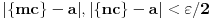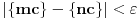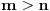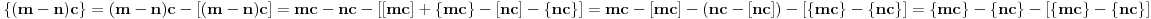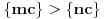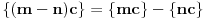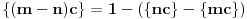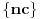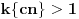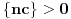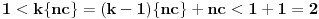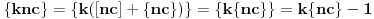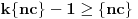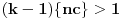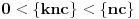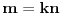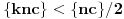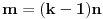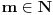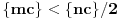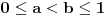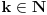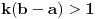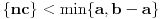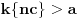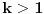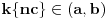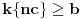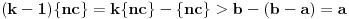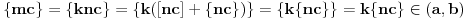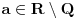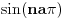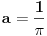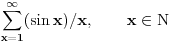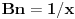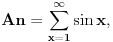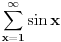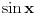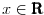|
|
[ markob15 @ 23.09.2010. 23:29 ] @
|
| Dakle interesuje me pitanje konvergencije reda :
(Posto sam retardiran i ne znam LaTeX napisacu kako znam i umem)
1. Beskonacni red (x=1 do beskonacno, x - prirodan br)
Opsti clan: sinx
*vec znam da red konvergira ali ne znam kako...t.j.na osnovu cega...kojom racunicom? (trebalo bi nesto preko parcijalnih suma)
2. red (x=0 do beskonacno, x - realan br)
opsti clan: sinx
**mislim da bi to trebalo da bude 0
Odgovor bi mi koristio sto pre jer uskoro imam ispit..
HVALA POZ! |
[ miki069 @ 24.09.2010. 00:26 ] @
Ispit iz čega?
Jeste li radili redove u okviru tog predmeta ili niste?
1. Postoje neke definicije. Treba da se znaju i razumeju.
2. Postoje neke teoreme. Treba da se znaju i razumeju.
3. Postoje neka pravila upoređivanja. Treba da se znaju i razumeju.
4. Postoje nekakvi kriterijumi za ispitivanje konvergencije redova, koji isto treba da se znaju, poželjno i razumeju:
- Dalamberov kriterijum,
- Košijev kriterijum,
- Kumerov kriterijum,
- Lajbnicov kriterijum i
- Integralni kriterijum.
5. Neki kriterijumi u primeni traže izračunavanje limesa, a samo jedan od njih i limesa i integrala, dakle:
6. Moraju se dobro znati limesi i integrali.
7. Tek onda može da se mašta o zadacima.
Konkretan primer može se uraditi, pošto nije tabličan, primenom integralnog kriterijuma i dobiće se ono što već znaš.
Konvergira.
Pošto ti se žuri, evo ti i brza literatura: http://www.elfak.ni.ac.rs/phpt...rana-poglavlja/redovi_text.pdf
[ markob15 @ 24.09.2010. 00:33 ] @
Kao prvo, hvala na odgovoru.
Predmet je varijanta analize (matematicki fakultet)
Redovi su radjeni, znam i razumem vecinu teorema, isto vazi i za kriterijume.
Sve tacke od 1. do 7. ispunjene.
tako da sam spreman da pocnem da mastam o zadacima ;)
ako ti nije problem da prilozis r-nje ?
NAPOMENA:
Funkcionalni redovi nisu radjeni...kao ni furijerovi i svi ostali koji slede...
[ miki069 @ 24.09.2010. 00:51 ] @
Pošto bi Dalamberov i Košijev kriterijum doveli do neodlučne situacije, jer bi rezultat odgovarajućih limesa bio 1, primenjuje se integralni kriterijum.
Integral (u granicama od 1 do + beskonačno) od sinx*dx je = -cos(x) od 1 do + beskonačno,
što je po Njutn-Lajbnicovoj formuli daje rezultat:
Limes(-cos(x)) - (-cos(1)), gde x teži u +beskonačno.
Taj rezultat je konačan broj iz intervala (-2,+2) i
zaključuje se da je integral konvergentan,
što znači da je početni red konvergentan.
[ markob15 @ 24.09.2010. 00:54 ] @
Ok hvala!
[ miki069 @ 24.09.2010. 01:13 ] @
Tek sad vidim da su: sin1, sin2 i sin3 pozitivni, a sin4, sin5, sin6 negativni i da zadatak nije baš tako naivan.
Dalamberov, Košijev i Kumerov kriterijum ispituju konvergenciju redova sa isključivo svim pozitivnim članovima (ili svim negativnim, pa se minus izvuče ispred reda) i ne mogu se ni primenjivati na ovaj zadatak.
Lajbnicov kriterijum rešava alternativne redove (negativan pa pozitivan ili obrnuto, ali jedan po jedan, a ne 3 pa 3), tako da ovo nije alternativni red, pa ne može ni Lajbnicov kriterijum. Kad bi on mogao doveo bi do apsurda, da red divergira, iako je što ti kažeš "viđeno" da konvergira.
Nisam načisto za integralni kriterijum da li ima ograničenja koja ostali kriterijumi imaju i da li sme da se primenjuje na ovaj zadatak. To je ona priča o teoriji, koja sad i meni nedostaje.
Ali ne brini, uključiće se neko drugi (recimo Nedeljko) i otkloniti neodumicu.
[ markob15 @ 24.09.2010. 02:08 ] @
Da u pravu si...glup sam sto nisam ranije primetio... ne moze ni integralni...
to se radi 100% preko parcijalnih suma.. i koliko se secam svodi se na to da red NE ZAVISI OD N t.j. ispadne neka obicna brojka...
samo mi nije jasno kako se sprovodi taj racun...
[ Cabo @ 24.09.2010. 09:13 ] @
Citat: markob15: Dakle interesuje me pitanje konvergencije reda :
(Posto sam retardiran i ne znam LaTeX napisacu kako znam i umem)
1. Beskonacni red (x=1 do beskonacno, x - prirodan br)
Opsti clan: sinx
*vec znam da red konvergira ali ne znam kako...t.j.na osnovu cega...kojom racunicom? (trebalo bi nesto preko parcijalnih suma)
2. red (x=0 do beskonacno, x - realan br)
opsti clan: sinx
**mislim da bi to trebalo da bude 0
Ajd da bar prečukam (klikni na formulu i videćeš kako sam je dobio):
1. 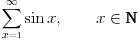 , tj. 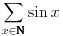 .
2. 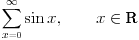 , tj. 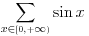 .
IZMENA: Jesi li probao adicione formule u prvom zadatku?
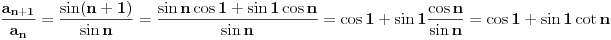
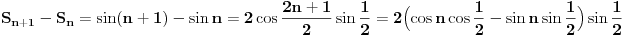
LOL vratiću se ovome ako budem imao vremena i ako me Nedeljko (ili neko drugi) ne pretekne.  [Ovu poruku je menjao Cabo dana 24.09.2010. u 10:39 GMT+1]
[Ovu poruku je menjao Cabo dana 24.09.2010. u 10:39 GMT+1][ Nedeljko @ 24.09.2010. 11:11 ] @
Alo, ljudi, ovi redovi divergiraju jer nije ispunjen neophodan uslov konvergencije reda da opšti član teži nuli.
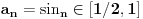 za one  koje je 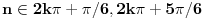 . Dakle, za 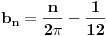 treba da bude 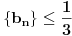 . Da vidimo. Uz oznaku 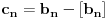 može li za neko  biti 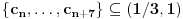 . Odgovor je negativan.
Naime, ako je 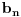 i 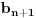 imaju različit ceo deo, onda je ceo deo od 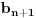 za jedan veći od celog dela od 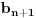 jer je 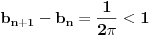 . No, tada mora biti 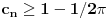 , pa je 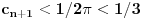 .
Ako je 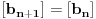 , onda je 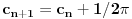 .
Ukoliko svi od brojeva 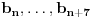 imaju isti ceo deo, onda je 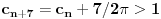 , što je nemoguće. Stoga, postoji bar jedan od brojeva 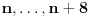 čiji je sinus veći od 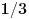 . Stoga niz 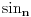 ne teži nuli, pa red divergira.
BTW, integralni kriterijum nije primenljiv jer opšti član nije monoton niz. Može se dokazati da je skup tačaka nagomilavanja niza 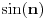 jednak celom segmentu 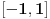 , što je posledica iracionalnosti broja  .
[Ovu poruku je menjao Nedeljko dana 24.09.2010. u 15:03 GMT+1][ Cabo @ 24.09.2010. 11:16 ] @
Citat: Nedeljko: Alo, ljudi, ovi redovi divergiraju
Haha, zbunilo me to što je rekao da „zna da konvergiraju“, pa rekoh da to piše u postavci. =) [ Nedeljko @ 24.09.2010. 13:57 ] @
Ako je 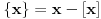 , onda važi:
Skup tačaka nagomilavanja niza 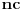 je jednak 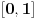 akko je c iracionalan broj.
Neka je 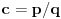 , 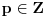 , 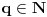 . Tada je 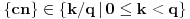 , pa pošto je taj skup konačan, skup tačaka nagomilavanja ne može biti 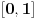 .
Neka je 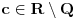 . Tada je 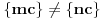 za 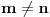 . Zaista, ako je 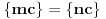 za 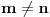 , onda je 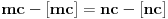 , pa je 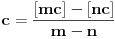 suprotno iracionalnosti broja  . Jasno je da zbog 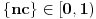 ovaj niz ima bar jednu tačku nagomilavanja 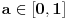 .
Neka je 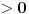 . Tada mogu naći različite 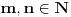 takve da je 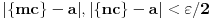 , pa je 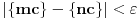 . Određenosti radi, možemo pretpostaviti da je 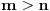 . Zbog
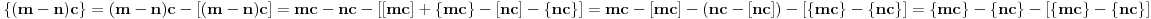
za 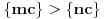 važi 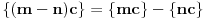 a u suprotnom 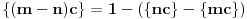 . Stoga je bar jedna od tačaka 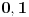 tačka nagomilavanja niza 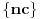 .
Ako je jedinica tačka nagomilavanja, onda se za bilo koje  može naći 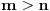 takvo da je 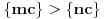 . No, onda je 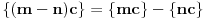 , pa je i nula tačka nagomilavanja. Dakle, nula je tačka nagomilavanja u svakom slučaju.
Drugi način da se dokaže da je nula tačka nagomilavanja je sledeći:
Neka je  proizvoljno i neka je  najmanji prirodan broj za koji je 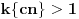 . Takav broj postoji (i veći je od 1) zato što je 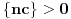 budući da je broj  iracionalan. Obzirom da je 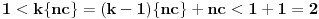 , važi 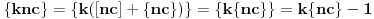 . Ako bi bilo 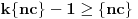 , onda bi bilo 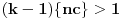 suprotno izboru broja  . Dakle, 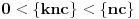 . Neka je 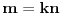 ako je 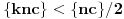 , odnosno 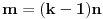 u suprotnom. Tada je 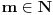 takav da je 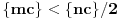 , pa je nula zaista tačka nagomilavanja.
Dokažimo sada samo tvrđenje.
Neka je sada 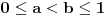 i 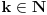 takvo da je 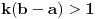 . Izaberimo takvo  da važi 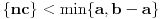 i neka je  najmanji prirodan broj za koji je 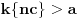 . Tada mora biti 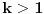 i 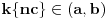 . Zaista, u suprotnom bi bilo 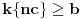 , odakle bi sledilo da je 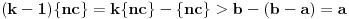 suprotno izboru broja  . No, tada za 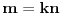 važi
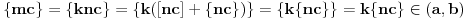 . [ Nedeljko @ 24.09.2010. 14:01 ] @
Neka je 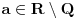 . Tada je prema prethodnom skup tačaka nagomilavanja niza 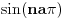 jednak 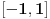 . Zadatak sa početka je specijalan slučaj za 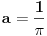 . [ markob15 @ 30.09.2010. 01:06 ] @
Geska ljudi zajebah se...
zapravo imao sam zadatak gde :
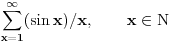 konvegira.
pa sam iz pogresne pretpostavke da se zadatak racuna preko abela t.j. 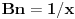 je monoton i ogranicen, => 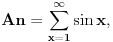 konvergira
medjutim zadatak se dokazuje preko dirihlea, t.j. potrebno je samo dokazati da je niz parcijalnih suma reda An ogranicen. A to stoji.
Tako da izvinite na maltretiranju.
P.S. sve vreme mi je bilo suludo kako 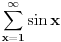 moze da konvergira kada niz 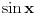 ocigledno divergira... mislio sam da nije mozda do prirodnih brojeva, posto taj skup nije gust (za razliku od realnog) pa dolazi do izvesnih pomeranja...
U svakom slucaju hvala na pomoci, svaki put se pozitivno iznenadim koliko na ovom forumu ima ucenih ljudi raspolozenih da izadju u susret raznim neznalicama i njihovim problemima. [ Cabo @ 30.09.2010. 17:32 ] @
Citat: markob15:
\sum_{x=1}^{\infty}(\sin x)/x,\qquad x\in\pmb{\hbox{N}}
Oftopik, u ovom primeru \pmb ( Poor Man's Bold) ne radi jer nije uključen amstex.
Za to je potrebno nešto ovako ( line break-ovi, čak i posle/pre tex BB tagova, su bitni!):
[ tex]
\input amstex
$$x\in\pmb{\hbox{R}}$$
\bye
[ /tex]
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|