[ kex21 @ 27.09.2010. 22:30 ] @
evo zadaci ispit treba mi rjesiti 2 4 5 6 8 zadatak zahvaljujem |
|
[ kex21 @ 27.09.2010. 22:30 ] @
[ atomant @ 27.09.2010. 23:50 ] @
Ne znam diskretnu matematiku, ali 6. zadatak nije tezak. Matematicka indukcija.
Dakle, 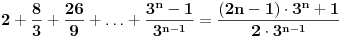 Proverimo da li tvrdjenje vazi za  : : 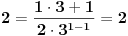 Vazi. Vazi.Pretpostavimo da tvrdjenje vazi za 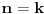 : : 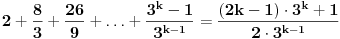 Dokazimo da vazi za 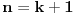 : :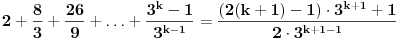 A to, kad se malo sredi izgleda ovako: 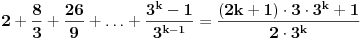 Podjimo od indukcijske hipoteze: 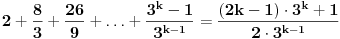 Na obe strane dodajmo 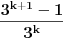 : :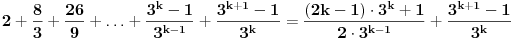 Sada bi trebalo da dokazemo da je: 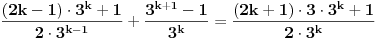 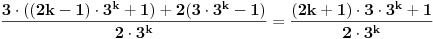 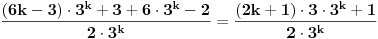 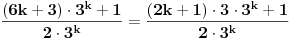 Q.E.D. [ miki069 @ 28.09.2010. 03:00 ] @
8. Zadatak:
An-6*An-1 + 9*An-2 = 1 An = Bn + Dn Bn je homogeni deo Dn je partikularni deo Bn - 6*Bn-1 + 9*Bn-2 = 0 Odgovarajuća diferencna jednačina je: r^2 - 6*r + 9 = 0. r1=3 i r2=3. Bn= C1*(3^n) + C2*(3^n)*n Pošto je na desnoj strani konstanta 1 onda je partikularni deo nezavisan od n: Dn=K, Dn-1=K i Dn-2 = K. K-6K + 9K = 1 K=1/4. An= C1*(3^n) + C2*(3^n)*n + 1/4. Ostaje još samo da se nađu konstante C1 i C2 iz početnih uslova. A0=2 sledi 2 = C1 + 1/4 A1=0 sledi 0 = 3C1 + 3C2 + 1/4 C1=7/4 , C2=-11/6 An= 7/4*(3^n) - 11/6*(3^n)*n + 1/4 [Ovu poruku je menjao miki069 dana 28.09.2010. u 08:47 GMT+1] [ miki069 @ 28.09.2010. 03:36 ] @
5. Zadatak:
18^111 = (10 + 8) ^111 = 10^111 + 111*(10^110)*8 + .... 8^111. Svi članovi osim zadnjeg imaju zadnju cifru 0 tako da 18^111 ima isti zadnju cifru kao i 8^111. 8^111 = (2^3)^111 = 2^333 2^1 = 2 2^2 = 4 2^3 = 8 2^4 = 16 2^5 = 32 2^6 = 64 2^7 = 128 2^8 = 256 2^9 = 512 2^10 = 1024 2^11 = 2048 2^12 = 4096 . . . 2^(4k+1) = ima zadnju cifu 2 2^(4k+2) = ima zadnju cifu 4 2^(4k+3) = ima zadnju cifu 8 2^(4k) = ima zadnju cifu 6 2^333 = 2^(4*83 + 1) pa je zadnja cifra 2. [ miki069 @ 28.09.2010. 03:50 ] @
5. Zadatak bez upotrebe binomne formule.
18^111 = (6*3)^111 = (6^111)*(3^111). 6 na bilo koji stepen ima zadnju cifru 6. 3^1 = 3 3^2 = 9 3^3 = 27 3^4 = 81 3^5 = 243 3^6 = 729 3^7 = 2187 3^8 = 6561 . . . 3^(4k+1) = ima zadnju cifu 3 3^(4k+2) = ima zadnju cifu 9 3^(4k+3) = ima zadnju cifu 7 3^(4k) = ima zadnju cifu 1 3^111 = 3^(4*27+3) i ima zadnju cifu 7. 6^111 ima zadnju cifru 6. 7*6 = 42, zadnja cifra je 2. [ petarm @ 29.09.2010. 13:53 ] @
@ Karlo
Za koji fakultet je ovaj ispit? Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|