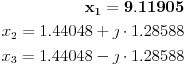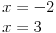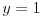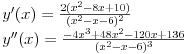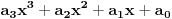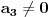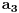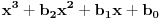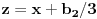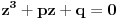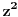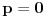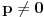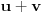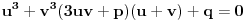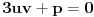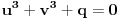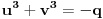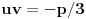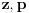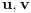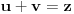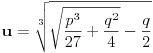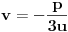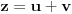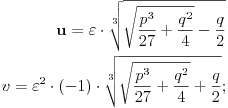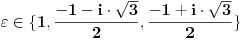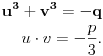|
|
[ capsela @ 30.09.2010. 14:58 ] @
|
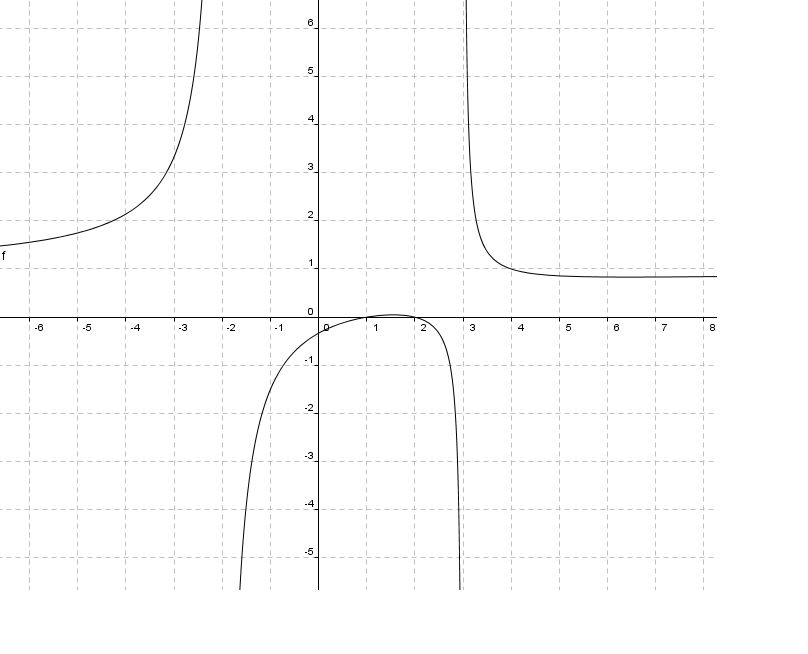
| Data je f-ja i treba ispitati njen tok i nacrtati grafik…
y=((x^2-3x+2))/(x^2-x-6)
Prvi izvod f-je dobija se da je:
y'=2(x^2-8x+10)/(x^2-x-6)^2
I fja raste za x iz intervala (-∞,4-√6) ∪ (4+√6, +∞)
Medjutim, dalje, drugi izvod f-je je:
y''=(((-4x^3+48x^2-120x+136)))/((x^2-x-6)^3)
Sada, da bismo odredili intervale na kojima je f-ja konveksna, odnosno konkavna, a samim tim i njene potencijalne prevojne tacke, treba da odredimo znak brojioca…
Medjutim, pokusavala sam naci nule gore navedenog polinoma, i primeniti deljenje polinoma, ne bih li dobila prostije polinome, podesnije za odredjivanje nule… medjutim, ne ide…. Mora da negde gresim…. Ako imate resenje, bila bih vam zahvalna…
|
[ atomant @ 30.09.2010. 15:53 ] @
Dobri su ti izvodi. Nule polinoma iz brojioca su:
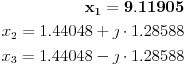
Ne mozes da odredis nule analiticki, na zalost. Mogu da ti nacrtam funkciju ako te interesuje kako izgleda (mada to verovatno umes i sama). [ capsela @ 30.09.2010. 20:14 ] @
aha... jeste li to koristili neke metode iz numericke analize, da biste dobili korene datog polinoma u brojiocu drugog izvoda? Kako onda objasniti odredjivanje intervala konveksnosti/konkavnosti, kada nije moguc analiticki pristup u resavanju istih!? :(
[ miki069 @ 30.09.2010. 21:02 ] @
Ispitaš znak drugog izvoda i videćeš da je on za X=9 pozitivan, a za X=10 negativan,
što znači da drugi izvod ima samo jednu realnu nulu Xp iz intervala (9,10).
Metodama povovljenja intervala, sečice ili tangente moglo bi se preciznije odrediti Xp, ali
to ti nije potrebno.
Pošto ne znaš precizno Xp, onda Yp proceniš da je iz intervala (Ymin, 1).
PT(Xp, Yp), gde Xp iz (9,10), a Yp iz (Ymin, 1).
Jesi li odredila gde funkcija preseca horizontalnu asimptotu?
Neki profesori i to traže. T(4,1) pripada i funkciji i HA.
Ne valjaju ti intervali monotonosti (opadanja i rašćenja funkcije),
iako su ti ispravni izvodi i extremne vrednosti.
Nisi vodila računa o vertikalnim asimptotama.
[Ovu poruku je menjao miki069 dana 01.10.2010. u 10:02 GMT+1]
[ capsela @ 01.10.2010. 11:08 ] @
uh, u pravu ste... nesto se gadno ne uklapa... domen je ocigledan... f-ja nije ni parna ni neparna. Imamo dve vertikalne asimptote
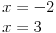
i horizontalnu asimptotu
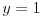
ok, presek sa ovom asipmtotom nije problem... nasli ste da je to tacka T(4,1)
znak fje, vidi se sa grafika... i to je ok...
medjutim, izvodi f-je su dobri..
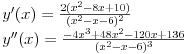
problem je, kako sada ustanoviti intervale monotonosti f-je???... ocigledno da sam napravila gresku kod prvog zakljucka da je opadajuca f-ja za x iz (4-√6,4+√6)
a jos vecu zabunu mi pravi kkao odrediti intervale konveksnosti/konkavnosti analiticki....
hocu da znam gde gresim...
 [ Cabo @ 01.10.2010. 13:47 ] @
Šta znači da je funkcija monotona? Šta je u tom slučaju ispunjeno? Prvo to razjasni. Nacrtaj grafik monotone funkcije.
Šta znači da je funkcija konveksna/konkavna? Šta onda važi?
Kada pronađeš odgovore na ta pitanja automatski ćeš doći do odgovora i na pitanje kako pronaći intervale monotonosti i konveksnosti/konkavnosti.
Opet se sve svodi na dobro poznavanje teorije.
[ Nedeljko @ 01.10.2010. 16:59 ] @
Znaš kako, jednačine trećeg i četvrtog stepena se mogu rešiti preko korenih funkcija, ali ti se na pismenom to najverovatnije ne traži na pismenom.
Prvo jednačinu 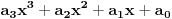 , 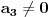 podeli sa 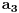 da bi dobila ekvivalentnu jednačinu sa vodećim koeficijentom jednakim 1, tj. oblika 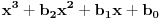 . Onda uvedi smenu 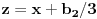 . Dobićeš jednačinu oblika
(1) 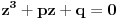 ,
tj. koeficijent uz 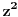 će biti 0. Slučaj kada je 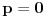 je trivijalan. Razmotrimo zato slučaj 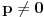 .
Sada zameni  sa 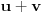 .
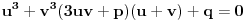 .
Uz uslov 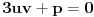 ova jednačina se svodi na 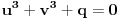 .
Dakle, treba rešiti sistem
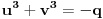 ,
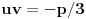 .
Jasno je da svako rešenje ovog sistema daje po jedno rešenje jednačine (1), a obzirom da za ma koje 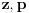 postoje 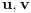 takvi da je 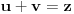 i 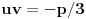 , time su obuhvaćena sva rešenja.
Dakle,
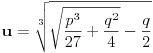 ,
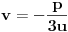 ,
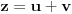 . [ capsela @ 03.10.2010. 13:48 ] @
Zahvaljujem na pomoci... Zaista je korisno...
[ Sini82 @ 04.10.2010. 15:06 ] @
Sva rješenja jednačine 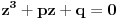 su oblika 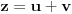 i vrijedi:
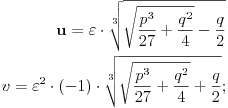
 je treći korijen iz jedinice tj. 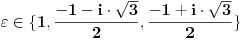 .
Može se direktno provjeriti da su na ovaj način zadani  i  rješenja sistema:
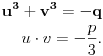 [ miki069 @ 06.10.2010. 23:25 ] @
Mislim da si me pogrešno razumela za intervale monotonosti.
Ispravan ti je prvi izvod i znak prvog izvoda.
Interval opadanja ti je u redu, ali kad iz njega isključiš X=3, jer je to vertikalna asimptota.
Interval rašćenja ti je u redu, ali kad iz njega isključiš X=-2, jer je to vertikalna asimptota.
[ capsela @ 07.10.2010. 17:07 ] @
Da, da,... sve je razjasnjeno... Mozda se niste najpreciznije izrazili u gore navedenom odgovoru, ali ne smeta... F-ja je ispitana, i uradjena... Naravno, znam da se iskljucuju malopre pomenute tacke (uostalom, ni ne mogu biti ukljucene zbog toga sto ne upadaju u sam domen f-je, a ujedno i zbog samih j-na asimptota)... Bunilo me je, zapravo, najvise to kako odrediti analiticki intervale konveksnosti i konkavnosti date f-je, ali Nedeljko i Sini82 su pomogli... U svakom slucaju, zahvaljujem svima na trudu...
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|