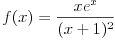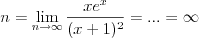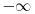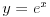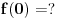[ capsela @ 09.10.2010. 14:20 ] @
|
[ Nedeljko @ 09.10.2010. 15:25 ] @
[ capsela @ 09.10.2010. 17:13 ] @
[ vtnnn @ 10.10.2010. 09:14 ] @
Ja cu malo biti off-topic, ali moram da pitam. Naime:
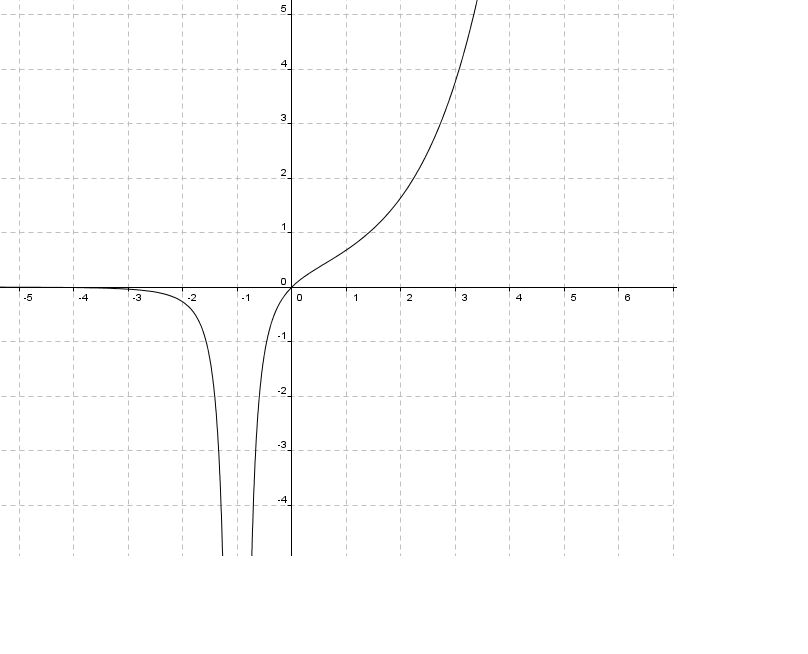
kako si napisao ove f-le i kako si nacrtao grafik - tj. u kojem/im programu/ima? [ capsela @ 10.10.2010. 19:40 ] @
'vtnn', pitanje je koga pitate!? ako pitate 'capselu', pogresili ste rod!
u svakom slucaju, potrebne informacije su na sledecem linku:... [ igorpet @ 10.10.2010. 20:38 ] @
[ miki069 @ 11.10.2010. 21:18 ] @
Prevojna tačka?
[ Kolins Balaban @ 12.10.2010. 09:09 ] @
[ Cabo @ 12.10.2010. 16:52 ] @
Citat: igorpet: Obzirom na mogucnosti LaTeX-a dosta je lep grafikon ispao Grafik, očito, nije crtan u 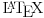 -u. (Mada nije da ne bi mogao da se nacrta još lepši. -u. (Mada nije da ne bi mogao da se nacrta još lepši. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|