[ zurrben @ 11.10.2010. 13:34 ] @
| Zanima me kakva su vasa razmiljanja o Gedelovom dokazu postojanja Boga? |
|
[ zurrben @ 11.10.2010. 13:34 ] @
[ Nedeljko @ 11.10.2010. 15:50 ] @
Kao i o svakom drugom "dokazu" postojanja/nepostojanja Boga. Može da se baci!
[ zurrben @ 11.10.2010. 17:04 ] @
Da li smatras da je dokaz matematicki nekorektan ili su aksiome "diskutabilne"?
[ westocean @ 12.10.2010. 15:01 ] @
U matematičkoj teoriji ne treba tražitni "nešto više". Matematika je vezana za odredjeni kontekst i van tog konteksta data teorija postaje neupotrebljiva. Zato ako neko i "dokaže matematički" da bog postoji/nepostoji taj dokaz će da važi samo u datom kontekstu odnosno pod uslovima teoreme. Po teistima bog je iznad svega tada je iznad uslova bilo koje teoreme pa je i dokaz bezvredan ako ne dokazuje da bog postoji. Ateista će opet da misli drukčije.
Kada je Gedel objavio taj rad i gde? [ Fitopatolog @ 12.10.2010. 15:31 ] @
Nije reč o dokazu te vrste. Gedelove teoreme, Tjuringov halting problem, Raselov paradoks nam poručuju da ispravnost neke stvari (ili njena definicija) ne može da se dokaže (izvede) preko te iste stvari. Sistem definicija-aksioma-teorema intuitivno izgleda OK ali se preko njega samoga to ne može potvrditi. Takođe, ne može se napraviti program kojim će se dokazati to da li bilo koji program na svetu radi OK ili ne...
[ westocean @ 13.10.2010. 09:26 ] @
Gedelove teoreme po mom mišljenju više govore da se egzistencija boga ne može izvesti matematičkim rezonovanjem nego što ide u prilog takvog dokaza. Ima jedna poslovica koja otprilike kaže da se više puta ponavljana izmišljotina na kraju percepira kao istina. Religija ne počiva na pozitivnim saznanjima nego na uverenjima. Ta uverenja se ponavljaju hiljadama godina nepromenjeno i postala su dogma. Matematika se bavi jasno definisanim objektima i operacijama nad tim objektima. Rezultati matematičkih operacija su ponovljivi i proverljivi od nezavisnih posmatrača. To nije slučaj sa religijskim "istinama". Kako bog nije definisan teško može biti predmet neke matematičke teorije a ako se definiše onda i nije neki bog. Neznam da li je Gedel bio religiozan ili ne ali ako su mu takva razmišljanja to i nije baš u skladu sa onim što je doprineo matematici. Da li postoji neki izvor za te tvrdnje o Gedelovim stavovima vezano za religiju?
[ Nedeljko @ 13.10.2010. 10:44 ] @
[ westocean @ 13.10.2010. 16:32 ] @
To su ta dokumenta! Ako je po definiciji "bog ono od čega se ne može zamisliti ništa veće" onda je Gedel kao matematičar trebao da podje od Peanovih aksioma od kojih jedna kaže da za svaki prirodan broj postoji sledbenik. Zaključak nepostoji najveći prirodan broj pa se uvek može "zamisliti nešto veće", dakle uzimajući u obzir definiciju koju je ponudio Gedel sledi da bog nepostoji.
[ zurrben @ 13.10.2010. 17:00 ] @
Gedel nije tako definisao Boga.Pogledaj jos jednom ontoloski dokaz.
[ westocean @ 13.10.2010. 18:49 ] @
Samo sam sledio link koji je postavio Nedeljko kao odgovor na moje pitanje. Primedbe ostaju bez obzira ko je zaista formulisao takvu definiciju. Ako ti kažeš da to nije Gedelova definicija u redu.
[ Nedeljko @ 13.10.2010. 20:46 ] @
Citat: westocean: To su ta dokumenta! Ako je po definiciji "bog ono od čega se ne može zamisliti ništa veće" onda je Gedel kao matematičar trebao da podje od Peanovih aksioma od kojih jedna kaže da za svaki prirodan broj postoji sledbenik. Zaključak nepostoji najveći prirodan broj pa se uvek može "zamisliti nešto veće", dakle uzimajući u obzir definiciju koju je ponudio Gedel sledi da bog nepostoji. Ne. Tvoja primedba samo znači da Bog nije u strukturi prirodnih brojeva. No, molio bih da se učesnici uzdrže od bilo kakvih komentara da li je religija u pravu ili ne, bavi li se istinama ili "istinama" i ostalim sadržajima koji ne odgovaraju forumu za matematiku. Tema je takva da vrlo lako može da sklizne na tu stranu, pa bih zamolio učesnike da povedu računa o tome. [ Nedeljko @ 13.10.2010. 21:05 ] @
Koliko vidim, Gedelova definicija Boga, je da ima sva pozitivna svojstva.
[ westocean @ 14.10.2010. 09:44 ] @
^Nedeljko:
Po teistima bog je "sveprisutan" pa bi morao biti i u bilo kojoj matematičkoj strukturi. Ako je to kako si napisao Gedelova definicija ista se može pobijati jednostanim rezonovanjem. Medjutim ulaženje u širu diskusiju zaista više nema veze sa matematikom. Tim pre što je to privatna stvar Gedela. Možda za neki forum koji se bavi religijom. [ zurrben @ 14.10.2010. 11:04 ] @
Citat: Ako je to kako si napisao Gedelova definicija ista se može pobijati jednostanim rezonovanjem. Kako? [ Nedeljko @ 14.10.2010. 12:50 ] @
To što si naveo je izvrtanje pojma sveprisutnosti. A što se jednostavnog rezonovanja tiče, mogao bi da ga navedeš, jer ako je rezonovanje u pitanju, onda ima veze sa matematikom.
[ westocean @ 14.10.2010. 12:58 ] @
U pravu si kad kažeš da tema izlazi iz okvira matematike. Prethodna dva komentara nas još više udaljavaju od matematike. Za matematiku je nevažno lakva je religijska uverenja imao Gedel. Uverenje u matematici nije diokaz.
[ zurrben @ 14.10.2010. 13:16 ] @
Gedel je koristio modalnu logiku za definiciju boga i za sam dokaz.
On definise osobinu G tako da G(x) vazi akko za svako g P(g) => g(x) gde P(x) znaci da je x pozitivna osobina Dalje on naziva osobinu G bozanskom i objekat x koji poseduje osobinu G bogom. Ovo jeste matematika i ako smatras da se moze pobiti jednostavnim rezonovanjem onda te molim da napises kako. [ Nedeljko @ 14.10.2010. 15:39 ] @
U okviru matematike je svakako:
1. Ispitivanje da li je izvođenje formalno korektno u modalnoj logici. 2. Ispitivanje da li je dati sistem aksioma protivrečan. Čini mi se da se westocean ne ustručava da daje nematematičke komentare kada je religija u pitanju, ali da izvrdava matematički deo. [ westocean @ 14.10.2010. 16:39 ] @
Ovde se nevide izvodjenja ni aksiomi osim one koju sam pomenuo pa nema šta ni da se ispituje.
Inače ako si matematičar trebao si primetiti da definicija data u komentaru pre tvog nije matematički korektna. Pa ni tu nema šta da se izvodi. Pojavljivanje simbola u toj definiciji nije najjasnije. Na primer mala i velika slova da li su u pitanju isti ili različiti objekti ili objekat i njegova pojava, zatim x je pozitivna osobina a nakon toga je x bog ako poseduje osobinu G. Da li je u definiciji => implikacija ili relacija pooretka, itd. Osim toga definicija nije dokaz. [ zurrben @ 14.10.2010. 16:46 ] @
Citat: Inače ako si matematičar trebao si primetiti da definicija data u komentaru pre tvog nije matematički korektna. Sta tacno nije korektno? [ Nedeljko @ 14.10.2010. 16:58 ] @
Citat: westocean: Ovde se nevide izvodjenja ni aksiomi osim one koju sam pomenuo pa nema šta ni da se ispituje. Inače ako si matematičar trebao si primetiti da definicija data u komentaru pre tvog nije matematički korektna. Pa ni tu nema šta da se izvodi. Pojavljivanje simbola u toj definiciji nije najjasnije. Na primer mala i velika slova da li su u pitanju isti ili različiti objekti ili objekat i njegova pojava, zatim x je pozitivna osobina a nakon toga je x bog ako poseduje osobinu G. Da li je u definiciji => implikacija ili relacija pooretka, itd. Osim toga definicija nije dokaz. Pa, tako kaži. Nisi ništa razumeo. OK. Na istoj stranici je dat link ka članku o modalnim logikama (ima ih više). To je neophodno predznanje. Ako sa time nisi upoznat, onda naravno da ne možeš razumeti izvođenje. [ Nedeljko @ 14.10.2010. 17:37 ] @
Uzgred, izvođenje ima više štamparskih grešaka.
[ westocean @ 14.10.2010. 19:43 ] @
Ti razumeš definiciju u kojoj se istim simbolom označavaju različiti objekti?
Nije mi namera ni da dokazujem ni da opovrgavam Gedelov "dokaz" jer kako si i sam napisao "Može da se baci!". I nije mi jasno šta ti bi da se odjednom okreneš za pun ugao i postaneš pobornik dokazivanja? [ Nedeljko @ 14.10.2010. 20:10 ] @
Dokaz može da se baci sa stanovišta tumačenja. Međutim, to ne znači da se on ne može logički analizirati.
U priloženom izvođenju je sve u redu zaključno sa redom Def2. U sledećem redu (Ax 4.) treba B zameniti sa P, a u naredna dva reda q i g treba zameniti sa x. Mislim da je onda u redu. [ westocean @ 14.10.2010. 20:45 ] @
Nisam komentarisao taj dokaz već definiciju koju je dao
Citat: zurrben: On definise osobinu G tako da G(x) vazi akko za svako g P(g) => g(x) gde P(x) znaci da je x pozitivna osobina Dalje on naziva osobinu G bozanskom i objekat x koji poseduje osobinu G bogom. Ovo nije "dobro definisano". [ Nedeljko @ 14.10.2010. 22:02 ] @
Pa, ni to nije nekorektna definicija.
P(x) - x je pozitivna osobina. G(x) - Za svaku osobinu g važi P(g) => g(x). Sve je u redu sa stanovišta korektnosti, mada ne odgovara Gedelovoj definiciji, jer se ovde nije vodilo računa o modalnim operatorima. Ovde se nigde ne definiše nikakav x (x je promenljiva), već osobine P i G. Ista promenljiva se može koristiti u više definicija. Zapisi P(x) - x je pozitivna osobina P(y) - y je pozitivna osobina P(g) - g je pozitivna osobina su potpuno ekvivalentni. Njima se definiše isključivo P i to na potpuno isti način. Dakle, gornji par definicija je potpuno isto što i P(g) - g je pozitivna osobina G(x) - Za svaku osobinu g važi P(g) => g(x). Sve je u redu sa stanovišta korektnosti. Pitanje: Koliko je 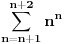 za za 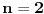 ? ?Napomena: Sve je napisano matematički korektno. Odgovor na pitanje je konkretan broj. [ westocean @ 14.10.2010. 23:55 ] @
Problem je što se x može tumačiti na različite načine a to nije u skladu sa dobrom definicijom. Ali ako se tumači tako kako si napisao onda nemam primedbi. Sa zbirom nije problem i tumačenje je samo jedno jer početne i krajnje vrednosti postaju konstnte dodeljene u startu.
[ Nedeljko @ 15.10.2010. 00:34 ] @
Na koje načine?
[ Nedeljko @ 15.10.2010. 00:36 ] @
[ westocean @ 15.10.2010. 10:19 ] @
Ako neko napiše "x pozitivna osobina" i odmah zatim "objekat x koji poseduje osobinu G" onda je potrebno dopunsko objašnjenje šta se pod tim podrazumeva jer je korišćen isti simbol u različitim kontekstima. Nevidim zašto je toliko teško, ako neko postavi pitanje, jednostavno uvesti dva različita simbola za dva različita objekta. Šta je tu problematično? Zašto? Čemu?
[ westocean @ 15.10.2010. 10:20 ] @
Odakle si izveo zaključak da izraz nema smisla? Napisao sam "tumačenje je samo jedno" a ti pišeš da je reč o funkciji. U čemu je onda problem? Ako je funkcija onda za dato n postoji "samo jedan" element kodomena.
[ Nedeljko @ 15.10.2010. 11:28 ] @
"gde P(x) znači da je x pozitivna osobina" - definiše se P.
"Dalje on naziva osobinu G bozanskom i objekat x koji poseduje osobinu G bogom" - definiše se Bog preko G. Ne vidim nikakvu dvosmislenost. Navedi bar još jedno smisleno tumačenje. Što se sume tiče, napisao si Citat: westocean: Sa zbirom nije problem i tumačenje je samo jedno jer početne i krajnje vrednosti postaju konstnte dodeljene u startu. Ispade da bi bilo više tumačenja kad početne i krajnje vrednosti ne bi postajale konstante u startu, pa je došlo do nesporazuma. [ westocean @ 15.10.2010. 13:54 ] @
U rečenici "gde P(x) znači da je x pozitivna osobina" je definisano i značenje x preko P jer se kaže "znači da je x pozitivna osobina".
Što se tiče zbira, kako bi ti nazvao veličinu čija vrednost se ne menja tokom izračunavanja? [ zurrben @ 15.10.2010. 14:09 ] @
Citat: westocean: U rečenici "gde P(x) znači da je x pozitivna osobina" je definisano i značenje x preko P jer se kaže "znači da je x pozitivna osobina" Ne, tako se definise P. [ westocean @ 15.10.2010. 14:14 ] @
Dobro, tu si definisao P a šta je onda x odnosno šta je pozitivna osobina?
[ Nedeljko @ 15.10.2010. 15:44 ] @
x je pomoćna promenljiva u definiciji za P.
[ westocean @ 15.10.2010. 16:30 ] @
Citat: Nedeljko: x je pozitivna osobina x je pomoćna promenljiva u definiciji za P. Hoćeš reći "pozitivna osobina" i "pomoćna promenljiva u definiciji za P" su sinonimi? [ Nedeljko @ 15.10.2010. 16:47 ] @
Ne.
[ Nedeljko @ 15.10.2010. 18:59 ] @
Nauči predikatski račun i teoremu o definicionoj ekstenziji, pa onda da polemišemo o definicijama.
[ westocean @ 15.10.2010. 20:19 ] @
De, de, Nedeljko ne žesti se. Samo si citiran.
I tako priča se razvodni te nikako da saznamo šta je to "pozitivna osobina". [ Nedeljko @ 15.10.2010. 20:33 ] @
Pa, što nisi čitao članak sa vikipedije? Tamo piše šta je pozitivna osobina. Zašto stalno pišeš napamet? Potrudi se malo oko kvaliteta svojih poruka.
[ westocean @ 15.10.2010. 20:41 ] @
Hebiga, neynam strane jeyike, begao sam iy [kole.
A što se tiče pisanja napamet nije tako, vidiš kako pažljivo čitam šta pišete. [ Nedeljko @ 15.10.2010. 21:27 ] @
OK, ne znaš engleski. Kaži tako. Pomoći ćemo ti.
Citat: Axiom 1: It is possible to single out positive properties from among all properties. Gödel defines a positive property rather vaguely: "Positive means positive in the moral aesthetic sense (independently of the accidental structure of the world)... It may also mean pure attribution as opposed to privation (or containing privation)." (Gödel 1995) Dakle, osobina je pozitivna ili ne u moralno estetskom smislu. Za pozitivnost je Gedel smatrao da zadovoljava prve dve aksiome izražene modalnom logikom. [ westocean @ 15.10.2010. 23:23 ] @
A tako, onda, na stranici Gödel's ontological proof je data definicija
Citat: Now we define a new property G: if x is an object in some possible world, then G(x) is true if and only if P(x) is true in that same world for all positive properties P. G is called the "God-like" property. An object x that has the God-like property is called God. koja je korektna. U ovoj definiciji x je objekat a P pozitivna osobina i nema zabune, trikova sa definicionim ekstenzijama itd. Sve je jasno i nedvosmisleno od prvog do poslednjeg slova a simboli imaju jedinstveno značenje. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|