Da napomenem, koordinate tacke B` trebaju biti 'u pravcu' vectora AB.

Neko misljenje? Imajte u vidu da tezim dobiti tacan rezultat s najmanjim brojem operacija, tako da je bilo kakav
savet dobrodosao.

Hvala

Trenutni položaj tačaka A i B jednoznačno definiše njihovu udaljenost dt,
tako da je dt suvišan kao ulazni podatak.

Nova udaljenost definiše dve nepoznate Xb i Yb.
To su nove koordinate tačke B.

Način rešavanje je pravljenje sistema 2 jednačine sa 2 nepoznate (Xb i Yb):

prva jednačina: udaljenost tačke A od B jednaka željenoj udaljeonosti dZ.
druga jednačina: pripadanje nove tačke B pravoj AB određenoj tačkama A i B.

Imaće 2 različita rešenja za tačku B.

Potrebno predznanje:
- udaljenost između 2 tačke,
- jednačina prave kroz 2 tačke,
- pripadanje tačke pravoj,
- rešavanje sistema 2 jednačine sa 2 nepoznate i
- kvadratna jednačina.

Naravno. Resavanjem jednacina nailazim na vrednost trenutne distance dt, te to nije suvisna informacija.
Ukoliko imas drugacije resenje, rad bih bio da pogledam.
Konacno resenje isto je kako sam i predlozio u prvom postu:

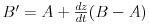
Jednostavnom manipulacijom dolazim do istog resenja B', ali sada preko B + ...

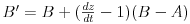
ali i ovo resenje ima prilicno veliki broj operacija. Ukoliko mislite da se isto moze dobiti "brze",
voleo bih da cujem kako.

Hvala

Ako je (B-A) = dt onda ti se krati dt sa zagradom (B-A)
i ostaje B' = A + dz, tako da je dt suvišan.

Jesu li tačke A i B u 2D ili u 3D?

Najelegantnije je da jednačinu prave A-B-B' pišeš u parametarskom obliku:
X = Xa + (Xb-Xa)*t
Y = Ya + (Yb-Ya)*t
i eventualno:
Z = Za + (Zb-Za)*t
I da ti jedina nepoznata bude parametar t, a ne X, Y i Z.
Kada nađeš parametar t za tačku B' onda si našao i tačku.

(B-A) podrazumeva (xb-xa, yb-ya), tako da je to drugacije od dt(jer je dt duzina, skalar).
Nisam siguran da razumem 'parametarski oblik' jednacine prave.
Recimo da je A(2, 4) i B(2, 6). Naci tacku B` na udaljenosti 5 od tacke A (na pravoj A-B-B`).

Kako postaviti jednacine? Hvala

Razumem da je mozda ocigledno, ali kako pronaci parametar t, i cemu on odgovara.
Koriscenje jednostavnog primera bi pomoglo.

Ako imas koordinate tacaka A(Ax,Ay) i B(Bx,By),


Moglo bi onda ovako:
B' = A + dz/dt(B-A) = A + dz/dt B - dz/dt A
= dz/dt B + (1-dz/dt)A
= B + (dz/dt - 1)B + (1-dz/dt)A
= B + (dz/dt - 1)(B - A)
Koliko vidim, ima jedna operacija vise, ali to je sad vec drugi problem.

Dosao sam do tog resenja. Iako ima +1 operaciju, ipak je manje u totalu jer je izrazeno preko B, a
usteda dolazi do izrazaja u postavci od preko 2D (100D, na primer).
Pitanje je mozemo li jos brze.
Hvala u svakom slucaju.