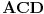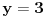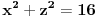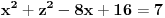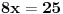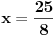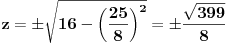resenje : Postoje!

Nije teško zamisliti dva pravougla trougla sa zajedničkom katetom AC, od kojih trougao ABC ima prav ugao kod A, a trougao ADC prav ugao kod C. Oni nisu u istoj ravni, nego stoje tako da je BD=4 (podrazumeva se da znaš da je trougao sa stranicama 3,4,5 pravougli).

Analitički: ako trougao ABC postaviš u pravougli koordinatni sistem tako da je A u koordinatnom početku, B na x-osi, a C na z-osi, lako ćeš iz uslova zadatka dobiti koordinate tačke D (A(0,0,0), B(4,0,0),C(0,3,0), D (x,y,z), pa imaš sistem od tri jednačine sa tri nepoznate).

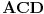
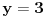
Iz uslova da je ugao prav zaključujemo da je . Dakle,

,

,

,

,

,

.

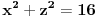
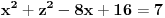
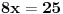
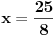
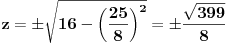
Da tražene tačke nisu postojale, dobio bi koren iz negativnog broja. Ovako smo našli rešenje, koje očigledno postoji.

_{[Ovu poruku je menjao Nedeljko dana 14.10.2010. u 15:00 GMT+1]}

_{[Ovu poruku je menjao atelago dana 26.10.2010. u 17:29 GMT+1]}