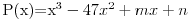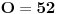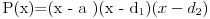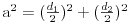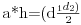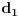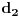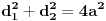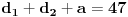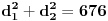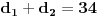[ lonelyrider_44 @ 15.10.2010. 10:02 ] @
|
| Polinom glasi:
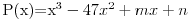
Treba odrediti koeficijente m i n, tako da nule polinoma budu dijagonale i stranica romba, chiji je obim 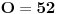 . .
Pokushavao sam na vishe nachina, ali uvek zavrshim sa nedovoljno jednachina spram broja nepoznatih. Generalno, koristio sam se pitagorinom formulom za pravougli trougao koji obrazuju polovine dijagonala i stranica, u nadi da preko stranice izrazim neku od dijagonala, pa tako dalje da sredjujem.
Probao sam da polinom predstavim na sledeca dva nachina:
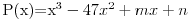
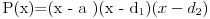
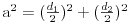
pa da sredjivanjem izraza i izjednachavanjem koeficijenata dobijem neshto od nepoznatih i tako postepeno reshim polinom. Medjutim, nisam uspeo. Da li greshim negde u postupku, ili mi nedostaje josh neka formula, kad je romb u pitanju ? Ne trazim da mi neko reshi ovo, samo uputstvo u kom pravcu da krenem, ako ovaj ne daje reshenja.
PS. Povrshinu romba sam odbacio, smatrajuci da ce mi samo zakomplikovati stvari
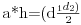
Hvala unapred! |
[ darkosos @ 15.10.2010. 21:33 ] @
Pa obim ti je 52, znaci da je a = O/4 = 52/4 = 13.
[ lonelyrider_44 @ 15.10.2010. 22:27 ] @
Da, nisam napisao da sam odredio a, na osnovu obima. Bash zato shto je a poznato, pokushavao sam da dovedem u vezu dijagonale i stranicu preko pitagorine teoreme. Poshto je a poznato, poznata je i jedna nula polinoma. Ostaju dve nule i koeficijenti m i n. Tu zapnem, kod 4 nepoznate. :)
[ Nedeljko @ 15.10.2010. 23:01 ] @
Pa, da bi
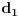
i
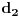
bile dijagonale romba sa stranicom

potrebno je u dovoljno da bude
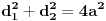
. Na osnovu Vijetovih pravila je još
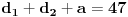
. Dakle,
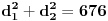
,
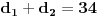
.
Dijagonale su dakle 10 i 24. Sada je lako odrediti polinom.
[ lonelyrider_44 @ 16.10.2010. 00:39 ] @
Odredjen. :)
Hvala ti puno
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.