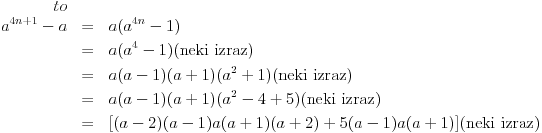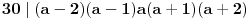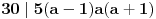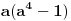Nije baš tako teško. Deljivost sa dva je očigledna. Ostaje deljivost sa 3 i 5. Rastaviti na činioce (dva puta razlika kvadrata).
Što se tiče deljivosti sa 3, odmah uočavaš, da ako već a nije deljiv sa 3, onda će jedan od činilaca (a^n -1),(a^n +1) biti deljiv sa 3, jer je a=3k+1 ili a=3k-1, pa binomni razvoj...
Deljivost sa 5 se razmatra slično, s tim da slučaj da je a=5k-2 ili a=5k+2 daje deljivost sa 5 zbog činioca (a^2n +1) za n neparano (jer a^2 je tada broj oblika 5t +4, pa je jedini sabirak u binomnom razvoju koji nije deljiv sa 5 4^n, a poslednja cifra tog broja je 4 sa onih +1 dobijamo 5), a iz jednog od činilaca (a^n -1),(a^n +1) za n parno (tada je poslednja cifra broja 4^n 6, pa ne može da se dobije iz (a^2n +1)).
Izvinjavam se što ne umem da koristim Latex, pa je ovo malo nečitko zapisano. A zbog svih slučajeva, možda indukcija i nije manje elegantan put.

A osim kongruencija, može i malo rastavljanja na činioce:



Među 5 uzastopnih celih brojeva, bar jedan je deljiv sa 2, bar jedan je deljiv sa 3 i bar jedan je deljiv sa 5, te stoga

Među 3 uzastopna cela broja, bar jedan je deljiv sa 2 i bar jedan je deljiv sa 3, te stoga

Kraj dokaza.

Hvala Farenhajt. Nemam poima kako mi nije palo napamet, kad sam indukcijom dokazivao za n=1, da ce se taj izraz pojavljivati stalno kao faktor...