Ovako bi trebalo,
primjena stolzovog teorema u kombinaciji sa binomnim obrascem...

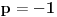
Za limes nema smisla.

Prvo primetimo da je

.

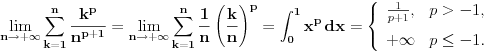
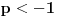
Odatle zaključujemo da za važi

.

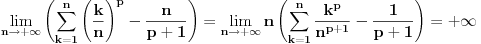
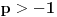
Takođe, odatle sledi da je za ispunjeno

,

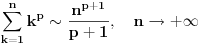
a samim tim i

.

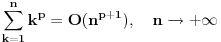
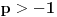
Neka je i

.

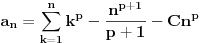
Važi

.

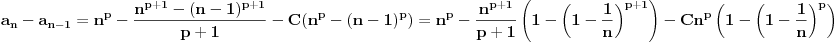
Na osnovu Tejlorove formule zaključujemo da je

,

odnosno,

.

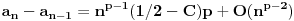
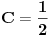
Za je

.

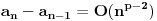
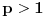
Odavde se zaključuje da je za ispunjeno

,

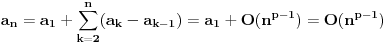
a samim tim i .

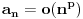
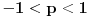
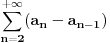
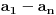
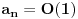
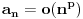
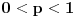
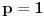
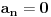
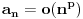
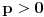
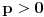
Za , zbog konvergencije reda , koji se svodi na niz , niz takođe konvergira. Odatle sledi da je , a samim tim i za . Za je očigledno , pa važi za sve. Stoga za važi

,

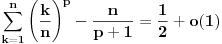
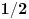
pa je traženi limes jednak za sve .

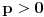
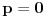
Za traženi limes je očigledno jednak 0.

Ostalo je još da se uradi za .

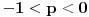
_{[Ovu poruku je menjao Nedeljko dana 02.11.2010. u 17:02 GMT+1]}

OK, odredimo ga za .

Neka je

.

Očigledno je . Dokažimo da je ovaj niz opadajući. Zaista,



za i . Dakle, dovoljno je da dokažemo da je za .

.

Dovoljno je dokazati da je brojilac pozitivan. On je oblika za i . Diferenciranjem se dobija da funkcija dostiže minimum u tački 1, pa je .

Dakle, niz je opadajući, pa je . Odatle sledi da je

,

pa je traženi limes jednak .

_{[Ovu poruku je menjao Nedeljko dana 02.11.2010. u 17:21 GMT+1]}

zahvaljujem....

@different
radio sam preko stoltza i rezultat je -beskonacno....;)

Evo jednostavnijeg rešenja za slučaj kada je .

Neka je . Iz

,

odnosno

,

.

Odavde sledi rekurentna formula

.

Indukcijom se lako dokazuje da je polinom stepena . Iz gornje formule sledi da je . Odatle i iz rekurentne formule sledi da je

,

odakle sledi da je traženi limes jednak 1/2.

Evo rešenja primenom Štolcovog stava za .



uslov za primenu Štolcovog stava je da imenilac strogo monotono teži beskonačnosti, što se kod nas svodi na .

.

Obzirom da je

,

zaključujemo da je .

_{[Ovu poruku je menjao Nedeljko dana 04.11.2010. u 14:03 GMT+1]}