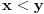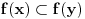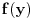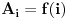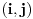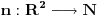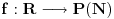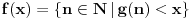[ Nedeljko @ 03.11.2010. 18:12 ] @
|
[ Sini82 @ 04.11.2010. 11:23 ] @
Jasno je da vrijedi za skupove iz f(R):
1.) Za svaka dva skupa A i B takva da je 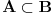 mora da postoji skup C tako da vrijedi mora da postoji skup C tako da vrijedi 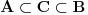 2.) f(R) nema ni najmanji ni najveci element 3.) B je podskup sa beskonacno mnogo elemenata jer u suprotnom ne bi vrijedilo 1.) 4.) A je podskup sa beskonacno mnogo elemenata jer bi u suprotnom ne bi vrijedilo 2.) Pošto skup R ima neprebrojivo mnogo elemenata, a skup f(R) prebrojivo mnogo (kada bi ih imao neprebrojivo mnogo sa gornjim osobinama i sam N bi ih imao neprebrojivo mnogo), traženo preslikavanje ne postoji. Nemoguće je utopiti neprebrojiv u prebrojiv skup. [ Nedeljko @ 04.11.2010. 12:00 ] @
Drago mi je da se neko zainteresovao za ovaj zadatak.
Citat: Sini82: Jasno je da vrijedi za skupove iz f(R): 1.) Za svaka dva skupa A i B takva da je 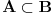 mora da postoji skup C tako da vrijedi mora da postoji skup C tako da vrijedi 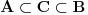 2.) f(R) nema ni najmanji ni najveci element 3.) B je podskup sa beskonacno mnogo elemenata jer u suprotnom ne bi vrijedilo 1.) 4.) A je podskup sa beskonacno mnogo elemenata jer bi u suprotnom ne bi vrijedilo 2.) Pretpostavljam da je 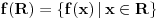 . U tom slučaju se slažem sa navedenim. Dakle, za svako . U tom slučaju se slažem sa navedenim. Dakle, za svako 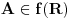 , skupovi , skupovi  i i 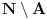 su beskonačni i za ma koje su beskonačni i za ma koje 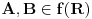 za koje je za koje je 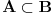 skup skup 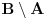 je beskonačan. je beskonačan.Citat: Sini82: Pošto skup R ima neprebrojivo mnogo elemenata, a skup f(R) prebrojivo mnogo (kada bi ih imao neprebrojivo mnogo sa gornjim osobinama i sam N bi ih imao neprebrojivo mnogo), traženo preslikavanje ne postoji. Nemoguće je utopiti neprebrojiv u prebrojiv skup. Kako si zaključio da je skup 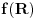 prebrojiv? Kako je njegova neprebrojivost u nesaglasnosti sa prebrojivošću prebrojiv? Kako je njegova neprebrojivost u nesaglasnosti sa prebrojivošću  ? ?[ Sini82 @ 04.11.2010. 16:00 ] @
Bio sam u frci sa vremenom, naveo sam ugrubo skicu dokaza, da vidim da li je dobro. Sada ću neke dijelove detaljnije da obrazložim.
Hvala Nedeljko što si me dopunio, nisam stigao sve da napišem. Da, tako je kako si napisao. Citat: Nedeljko: Kako si zaključio da je skup f(R) prebrojiv? Kako je njegova neprebrojivost u nesaglasnosti sa prebrojivošću N? Pretpostavimo suprotno, da je f(R)={f(x)|x 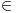 R} neprebrojiv. R} neprebrojiv. Tada postoji familija skupova 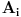 , , 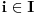 . .  je skup indeksa, prema našoj pretpostavci neprebrojiv. je skup indeksa, prema našoj pretpostavci neprebrojiv. 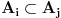 , , 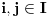 . Jasno je da je . Jasno je da je 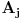 \ \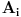 beskonačan skup (u suprotnom ne bi postojao skup beskonačan skup (u suprotnom ne bi postojao skup 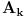 tako da vrijedi tako da vrijedi 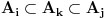 , za svako i i j iz skupa indeksa , za svako i i j iz skupa indeksa  ). Jasno je da je svaki od ovih skupova beskonačan kao i njihovi komplementi u N što takođe slijedi iz osobina (R,<) i definicije funkcije f. ). Jasno je da je svaki od ovih skupova beskonačan kao i njihovi komplementi u N što takođe slijedi iz osobina (R,<) i definicije funkcije f.Za svaka dva indeksa i i j iz skupa  , , 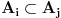 , može se uzeti element , može se uzeti element 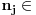 N koji pripada skupu N koji pripada skupu 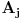 \ \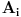 . Na taj način formiran skup { . Na taj način formiran skup {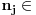 N| N|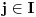 } iz lanca skupova } iz lanca skupova 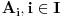 je neprebrojiv. je neprebrojiv. { 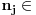 N| N|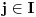 } }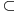 N je u kontradikciji sa prebrojivošću skupa N. N je u kontradikciji sa prebrojivošću skupa N.[ Nedeljko @ 04.11.2010. 16:21 ] @
[ zurrben @ 04.11.2010. 22:44 ] @
Kako R i P(N) imaju istu kardinalnost to postoji bijekcija f: R->P(N) ,tako da je jedino pitanje monotonost takve funkcije
Dalje definisimo funkciju f1:R->P(Q) tako da je f(x)={q|q<=x} Posto N i Q imaju istu kardinanost to postoji bijekcija g:N->Q Dalje mozemo definisati funkciju f2: P(Q) -> P(N) takvu da za svako A podskup Q f2(A)={n | n element N i g(n) element A}(tj. g^-1 (A) ) kako je kompozicija dve monotone funkcije takodje monotona to je i funkcija f= f1◦f2 takodje monotona Izvinjavam se sto ne koristim LATEX posto sam relativno nov na forumu i nisam stigao da ga pogledam. Ovo sto sam napisao meni deluje na prvi pogled tacno, mada sam dosta umoran i moguce da sam nesto prevideo, ispravite me ako gresim. [ Nedeljko @ 04.11.2010. 22:54 ] @
[ Sini82 @ 06.11.2010. 10:59 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|