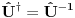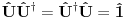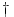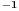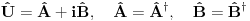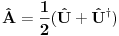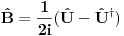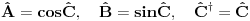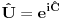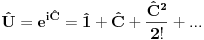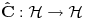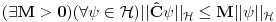[ petarm @ 04.11.2010. 13:03 ] @
|
[ Nedeljko @ 04.11.2010. 13:41 ] @
Da bi uopšte govorio o sinusu i kosinusu operatora, odgovarajući redovi moraju da konvergiraju, što u opštem slučaju nije tačno, ali je svakako tačno za ograničene operatore. Sinus i kosinus ograničenog ermitskog operatora jeste ograničen ermitski operator.
[ petarm @ 04.11.2010. 14:28 ] @
[ Nedeljko @ 04.11.2010. 20:06 ] @
Da, s tim da verovatno postoje i neki opštiji uslovi pod kojima priča prolazi.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|