[ Sini82 @ 06.11.2010. 21:40 ] @
| Kako se dokazuje da ne postoji prirodan broj sa beskonačno mnogo cifara? |
|
[ Sini82 @ 06.11.2010. 21:40 ] @
[ westocean @ 07.11.2010. 08:27 ] @
Kako je svaki prirodan broj konačan mora da ima i konačan broj cifara u bilo kojoj reprezentaciji. Realni brojevi nemoraju imati konačan broj cifara u nekim reprezentacijama. Na primer 1/11 se u decimalnoj notaciji nemože predstaviti konačnim brojem cifara. Ali u sistemu sa brojnom osnovom 11 to je broj sa konačnim brojem cifara, 1/1011 = 0.111,
[ Nedeljko @ 07.11.2010. 10:12 ] @
Citat: Sini82: Kako se dokazuje da ne postoji prirodan broj sa beskonačno mnogo cifara? Indukcijom. Prirodan broj n nema više od n cifara zato što prirodan broj 1 ima jednu cifru, a k+1 ima najviše jednu cifru više od k. [ westocean @ 07.11.2010. 10:42 ] @
Postavljeno pitanje je veoma zanimljivo. Ako se reprezentacija brojeva proširi na neke nestandardne osnove tada neki prirodni brojevi ne bi morali da imaju konačan broj cifara.
[ Nedeljko @ 07.11.2010. 13:18 ] @
Naravno da je mislio na desetični pozicionoi sistem.
Normalno da možeš pustiš mašti na volju, ali nema nikakve potrebe nizakakvim sistemom u kome bi zapis prirodnih brojevai bili beskonačni. [ westocean @ 07.11.2010. 13:51 ] @
Indukcija na koju se ti pozivaš zavisi od osnove brojnog sistema koji koristiš. Probaj to da dokažeš u brojnom sistemu sa osnovom 43/3. Koliko tada cifara imaju nama tako dragi brojevi 5 ili 10 ?
[ Sini82 @ 07.11.2010. 21:16 ] @
Može li se dokazati na neki drugi način, osim indukcijom? Za dekadni brojni sistem.
[ Nedeljko @ 07.11.2010. 21:26 ] @
A u čemu je problem sa ovim načinom?
[ Cabo @ 07.11.2010. 22:31 ] @
Beskonačnost! Nijedna druga stvar nije toliko pokrenula ljudski duh. Citat: westocean: Probaj to da dokažeš u brojnom sistemu sa osnovom 43/3. LOL osnova brojevnog sistema mora biti prirodan broj. [ westocean @ 07.11.2010. 22:31 ] @
Neka je dat prirodan broj n i pretpostavimo da n u decimalnoj notaciji ima beskonačno mnogo cifara. Tada je
n = x0100 + x1101 + ... + xr10r + ... i red sa desne strane divergira, kontradikcija jer je n konačan. [ westocean @ 07.11.2010. 22:38 ] @
Cabo: LOL osnova brojevnog sistema mora biti prirodan broj.
Zašto mora? Šta fali da se u prethodnom razvoju umesto 10 stavi na primer 1/2 ? [ Cabo @ 07.11.2010. 22:42 ] @
Hahahahahh...
Pa kako ćeš da imaš „pola cifre“? /facepalm [ westocean @ 07.11.2010. 23:08 ] @
Evo ovako:
1/210 = 101/2 Ostalo je jednostavno. Možeš koristiti kao osnovu čak i kompleksne brojeve (kako mi se čini ti spremaš neki ispit na temu kompleksne funkije?). Medjutim sa nekim osnovama može biti problema jer predstavljanje brojeva sa takvom osnovom nije jednoznačno. [ Nedeljko @ 08.11.2010. 04:08 ] @
@Cabo
Osnova može biti bilo koji kompleksan broj, a skup cifara može biti bilo koji skup kompleksnih brojeva. Na srpskom jeziku nešto o tome možeš naći u knjizi "Realni brojevi" Milojice Jaćimovića. Recimo, Knut je dokazao da se svaki kompleksan broj može prikazati na jedinstven način u sistemu sa osnovom 1-i sa skupom cifara {0,1}. [ Sini82 @ 09.11.2010. 20:02 ] @
Citat: westocean: Postavljeno pitanje je veoma zanimljivo. Ako se reprezentacija brojeva proširi na neke nestandardne osnove tada neki prirodni brojevi ne bi morali da imaju konačan broj cifara. Možeš li prevesti neki prirodan broj iz dekadnog brojnog sistema u brojni sistem sa nekom drugom osnovom tako da njegov zapis u tom brojnom sistemu ima beskonačno mnogo cifara (primjera radi može i u brojni sistem sa osnovom 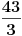 )? )?Citat: Nedeljko: A u čemu je problem sa ovim načinom? Ni u čemu. Zanima me može li da se dokaže na neki drugi način bez pozivanja na princip matematičke indukcije? Citat: Nedeljko: Osnova može biti bilo koji kompleksan broj, a skup cifara može biti bilo koji skup kompleksnih brojeva. Na srpskom jeziku nešto o tome možeš naći u knjizi "Realni brojevi" Milojice Jaćimovića. Recimo, Knut je dokazao da se svaki kompleksan broj može prikazati na jedinstven način u sistemu sa osnovom 1-i sa skupom cifara {0,1}. Ima li išta od toga u elektronskom obliku na srpskom jeziku da se može naći na internetu? [ westocean @ 10.11.2010. 08:01 ] @
Primenjujući beta-ekspanziju broja 10 uz osnovu 11/10 dobije se
1010 = 111...11/10 pa sa ovom osnovom broj 10 ima beskonačno mnogo cifara. [ Sini82 @ 10.11.2010. 20:21 ] @
[ westocean @ 11.11.2010. 08:21 ] @
Suma nije beskonačna samo je a0 = 0, i ima beskonačno mnogo jedinica u razvoju.
1010 = 111...1011/10 Pa je 1/(1-10/11) - 1 = 10, što sam imao na umu ali sam "zaturio" 0. [ Sini82 @ 11.11.2010. 10:26 ] @
Sada je u redu, još samo jedna mala ispravka:
Citat: westocean: 1010 = 111...1011/10 1010 = 111...1010/11. Neka imamo zapis prirodnog broja  u nekoj bazi u nekoj bazi  sa ciframa sa ciframa 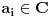 (gdje je C skup cifara): (gdje je C skup cifara): 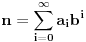 . .Imam tri pitanja: 1. Kada je baza 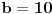 biramo biramo 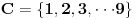 , baza , baza 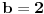 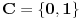 itd. Kako biramo skup cifara itd. Kako biramo skup cifara  ako je baza cijeli, racionalan, iracionalan, kompleksan broj; konkretno u našem slučaju kada je ako je baza cijeli, racionalan, iracionalan, kompleksan broj; konkretno u našem slučaju kada je 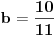 ? ?2. Pod kojim uslovima je suma reda 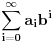 prirodan broj? prirodan broj? 3. Kakav je zapis prirodnog broja  u bazi u bazi  ? Da li može biti konačan ili je uvijek beskonačan? Da li je ako je beskonačan i periodičan? ? Da li može biti konačan ili je uvijek beskonačan? Da li je ako je beskonačan i periodičan?Unaprijed hvala na odgovorima. [ westocean @ 11.11.2010. 14:16 ] @
Cifre se mogu birati ovako {0, 1, ..., floor(b)} (ili čak {0, 1, ..., floor(b+1/2)}). Na primer ako je osnova 43/3 tada su cifre iz skupa (0, 1, ..., E}.
Algoritmi za konverziju brojeva se mogu pronaći u mnogim knjigama. Na primer Malešević, "Uvod u sistemsko programiranje I". A teorija iza toga je teorija redova o čemu takodje postoji dosta literature. Knut je u svojoj knjizi "The art of computer programming" Vol. 2, Seminumerical Algorithms izložio više primera sa različitim osnovama. Da ne bih petljao evo jednog primera sa kompleksnom osnovom: (11210.31)2i = 1*16 + 1*(-8i) + 2*(-4) + 1*(2i) + 3*(-i/2) + 1*(-1/4) = 31/4 - 15i/2 Za beta-ekspanziju u praksi se koriste dva dobro poznata postupka, pohlepna ekspanzija i lenja ekspanzija. Ova dva postupka nemoraju dati isti zapisa. Na primer ako je ß = (1 + Sqrt[5])/2 tada za x = 1 se dobije 1 = 11ß - (pohlepni postuopak) 1 = 0(1)infinityß - (lenji postupak) Za utvrdjivanje da li za neki broj postoji peridična beta-ekspanzija o tome nešto govore radovi vezani za Poisot i Salem-ove brojeve. Što se tiče jedinstvenog prikaza tu je interesantna teorema koja kaže da ako je 1 < ß < (1 + Sqrt[5])/2 i 0 < x < 1/(ß - 1) tada postoji aleph1 različitih ekspanzija. [ MajorFatal @ 17.01.2011. 02:20 ] @
Mogu li da biram Pi za osnovu brojnog sistema? Koje bi bile cifre? Kako bi izgledala tablica mnozenja?
Mora li broj da bude osnova brojnog sistema ili moze recimo neka funkcija? [ SrdjanR271 @ 17.01.2011. 03:20 ] @
[ MajorFatal @ 17.01.2011. 06:11 ] @
Hvala.
[ Sini82 @ 17.01.2011. 14:11 ] @
[ MajorFatal @ 17.01.2011. 20:06 ] @
Mozda 0,1,2 i onaj ostatak iza decimale kao posebna cifra, al posto sam ovo i onako bezveze pitao necu da lupam glavu...mada, dal bi bilo prostih brojeva ;)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|