Je li ovo nikoga ne zanima?

Ako nekoga zanima, mogu ja da okačim rečenje.

Mene zanima, samo nemam vremena ni literature da se podsjetim teorije mjere i posvetim rješavanju postavljenog zadatka. Nedeljko, ako ti ne predstavlja problem mogao bi da postavis rješenje.

Pa, evo skice:

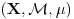
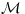
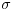
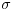
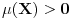
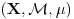
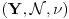
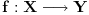
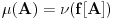
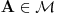
Razmatraćemo samo merljive prostore kod kojih je -algebra na , a -aditivna mera takva da je i da je mera svake tačke 0. Pretpostavljaćemo da je na definisana topologija takva da je kompletiranje neke Borelove mere. Jasno je da je svaki takav merljiv prostor neprebrojiv. Takve prostore i zvaćemo izomorfnim ako postoji bijekcija koja je Borelova u oba smera i takva da je za svaki . Jasno je da je to relacija ekvivalencije.

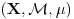
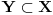
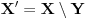
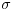
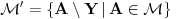
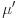
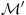
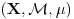
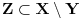
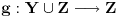
Pretpostavimo sada da je jedan takav prostor i da je najviše prebrojiv. Na skupu dobro su definisani -algebra i odgovarajuća mera kao restrikcija mere na familiju . Taj prostor je izomorfan sa . Zaista, obzirom na neprebrojivost skupa , postoji prebrojiv . Naravno, postoji i bijekcija . Tražena bijekcija data je sa



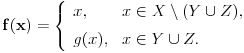
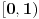
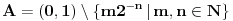
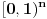
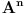
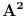
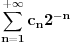
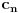
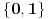
Stoga je prostor obrazovan od skupa snabdevenog Lebegovom merom izomorfan sa prostorom obrazovanim od skupa takođe snabdevenog Lebegovom merom. Samim tim je izomorfno sa . Da bismo dokazali da je izomorfno sa primetimo najpre da su elementi skupa brojevi oblika , gde je čiji je svaki član u skupu i koji ima i nulu i jedinicu na beskonačno mnogo mesta. Dakle, elemente tog skupa možemo poistovetiti sa takvim nizovima. 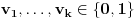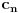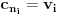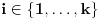Pritom će za ma koje različite prirodne brojeve i ma koje mera skupa svih nizova kod kojih je za sve jednaka . 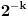Odavde se lako zaključuje da je taj prostor idempotentan, jer Dekartovi proizvodi baznih merljivih skupova imaju odgovarajuću meru.

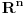
Ostatak sledi iz činjenice da je za svako prostor prebrojiva disjunktna unija translata prostora .

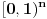
Svaka čast.