Prvo, 6a+2 je 2(3a+1), a ne 3(2a+1).

NZS(4,5,6,7)=420

Iz x=4a+2 množenjem sa 105 dobija se da je 105x=420a+210.
Iz x=5b+2 množenjem sa 84 dobija se da je 84x=420b+168.
Iz x=6b+2 množenjem sa 70 dobija se da je 70x=420c+140.
Iz x=7d množenjem sa 60 dobija se da je 60x=420d.

Oduzimanjem poslednje dobijene jednačine od prethodno dobijenih dobija se da je

60x=420d
45x=420(a-d)+210
24x=420(b-d)+168
10x=420(c-d)+140

Oduzimanjem poslednje dobijene jednačine od prethodnih odgovarajući broj puta, dobija se

0=420(2d-c)-840
10x=420(c-d)+140
5x=420(3d+a-4c)-350=420(3d+a-4c-1)+70
4x=420(b+d-2c)-112=420(b+d-2c-1)+308

Oduzimanjem poslednje jednačine od pretposlednje dobijamo da je

x=420(2d+a-b-2c)-238=420(a-b-2c+2d-1)+182

Sada treba proveriti da li broj 182 zadovoljava navedene uslove. Ostaci mu jesu toliki koliki treba da budu i svako rešenje mora biti oblika 420k+182. Lako se proverava da svako od takvih rešenja zadovoljava tražene uslove.

Ovako,
neka je x- ukupan broj knjiga. Cinjenica da se pakovanjem knjiga po 4, odnodno 5 , odnosno 6, dobijaju uvek dve knjige viska, moze se reprezentovanti sledecim matematickim zapisom:
xmod4=2
xmod5=2
xmod6=2

i konacno, kada se pakuju po 7, nema viska:

xmod7=0 (odnosno, ukupan broj knjiga je neki broj deljiv sa 7)

dalje, gore napisane formulacija, ekvivelatne su sledecim:

x=4a+2
x=5b+2
x=6c+2
x=7d
gde su a,b,c,d, neki briojevi iz skupa Z ( ili preciznije N).

izrazavanjem tih brojeva preko x, dobijamo



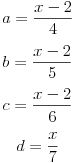
odavde sledi da, ako obelezimo sa m=x-2, vazi:

4|m i 5|m i 6|m

najmanji broj, koga dele ova tri broja je 60. medjutim, ako zamenimo u poslednem izrazu, videcemo da 58 (=60-2) nije deljivo sa 7. Ispitajmo sada koji sledeci broj dela ova tri (4,5,6).. to je 120. opet imamo da je x-2=120 => x=122
ni 122 ne moze se podeliti sa 7 a da se dobije ceo broj.
medjutim, kada je m=180, x=182, a 182 je deljivo sa 7! :)

dakle, najmanji broj knjiga koji se nalazi na stolu je 182
da proverimo: ako pakujemo knjige po 4 => 182/4= 45 i ostatak 2
ako pakujemo knjige po 5 => 182/5= 36 i ostatak 2
ako pakujemo knjige po 6 => 182/6= 30 i ostatak 2

i to je to!

Najmanji broj knjiga koje ce biti na stolu je najmanji broj oblika , koji je djeljiv sa 7, tj. takav da je tj. .

Tražimo neparne brojeve koji su djeljivi sa 7. To su: 7, 21, 35, 49, ...
tada uzima vrijednosti: 3, 10, 17, 24,...
Brojevi knjiga na stolu su: 182, 602, 1022, 1442, ...

_{[Ovu poruku je menjao Sini82 dana 10.11.2010. u 15:37 GMT+1]}

hvala na pomoci, i rjesenju. Sini, 122 nije djeljivo sa 7..... pa se taj broj ne moze uzeti kao rjesenje... ostali zadovoljavaju uslove zadatka.

@Kolins Balaban:

Hvala na ispravci, greška u kucanju: .