kosinusna teorema:



ti imas dato c zatim i kad to sve pouvrstavas u gornju formulu, dobit ces koliko ti je .

i na kraju trebas rijesiti sistem jednacina

gdje x dobijes na prethodno opisani nacin

Jao nisam nista skontao.

Nisam ucio rijesavanje sistema sa KVADRATNIM JEDNACINAMA sa dvije nepoznate sa kvadratom, pa ako moze to da pojasnis, ili samo rijesi taj sistem, valjda ja skontam kako si dosao do rijesenja. Jos jednom hvala

Ako neko moze da rijesi zadatak do sutra navece bio bi mu zahvalan, posto mi je prekosutra pismena a taj se zadatak pojavljuje.

a je l si cuo za nesto sto se zove smena? ako imas izraz oblika i onda iz druge jednacine izrazis npr a preko b i to vratis u prvu jednacinu, pa dobijes i eto ti jednacine koja se svodi na kvadratnu, i pritom ima jednu nepoznatu (b). Je l sad umes da resis zadatak?

Ovo je druga godina srednje skole, cini mi se...

Prvo, kosinusna teorema glasi



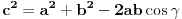
Drugo, kad uvrstis sve poznate velicine u ovu jednakost, dobices da je

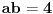
Dakle, mozes da resavas sistem dve jednacine sa dve nepoznate:




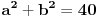
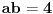
Pokusaj sad. Na raspolaganju su ti

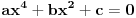
-metoda zamene (izrazis jednu od nepoznatih iz druge jednacine i uvrstis u prvu; obavezno odradi ovaj deo ,tek da vidis zasto nije 'zgodan' u ovom konkretnom zadatku, iako je korektan; ovde se podrazumeva da umes da resis bikvadratnu jednacinu oblika - prelistaj svesku, obradjena je odmah iza kvadratne; o ovome ti je atomant govorio)

-metoda 'snadji se' i napravi kvadrat zbira i kvadrat razlike, sto ce te dovesti do novog, neuporedivo jednostavnijeg sistema po nepoznatim i (preproucena verzija :) )

Napisi nam sutra resenje :)

Kako god uradim bikvadratnu jednacinu ne zadovoljavam ono a2 + b2 = 40

Sto se tice drugog nacina, njeg ne znam il ne razumijem pa bil ga mogao uraditi ako ti nije problem.

Kako, bre?

Kako ti glasi bikvadratna? Da bi otkucao koristi x^2 (ova 'kapica' je na shift+6)

cekaj, ako si dobio:

i , da li mozes dati sistem napisati ovako

(jednacini smo na obe strane dodali po )


sad znas da je:

*
a odavdje je , pa to zamjenis u jednacini * i dobit' ces kvadratnu jednacinu. imat' ces po dvije vrijednosti za a i b .

Naravno, tako je dobijen kvadrat ZBIRA. Zasto ne i kvadrat razlike? Bice jos jednostavnije...

Iz jednačine dobijamo dvije jednačine i .

Riješićeš dva sistema kvadratnih jednačina:

________________
i

________________.

Dobićeš četiri uređena para za skup rješenja zadanog sistema kvadratnih jednačina.

II način:

Smjenom i uvrštavanjem u jednačinu dobijamo bikvadratnu jednačinu . Njenim rješavanjem i uvrštavanjem u smjenu dobićeš tražena rješenja.

Evo kako vidite uradio sam pomocu kvadrata razlike. Međutim kad i uglove izračunam njihov zbir nije 180° Mozda sam pogriješio gdje u izradi, eto ko ima vremena neka malo pregleda. Još jednom hvala vam svima za pomoć.

zaista ne znam u cemu je problem..

primenom kosinusne teoreme dobija se da je

resimo sistem


dobro si dobio da je (svodjenjem na kvadrat razlike)
i da je prihvatljivo resenje za b,

zamenom u jednacini , za a dobijamo da vazi

zamenom u pocetnim jednacinama sistema dobija se da su a i b korektni:


tako da su stranice datog trougla

Takva sam i ja riješenja dobio, samo što sam ih ja još pretvorio u decimalne brojeve gdje je
a = 6,24 i b = 0,6

Moguće je da sam se zeznuo kod kada sam taj zadatak radio sa cosinusnom teoremom.

Pa, ne vidi se najbolje, ali vidim da si napravio taj kvadrat razlike koji sam ti pomenula, a i brojevi ti izgledaju OK.

A evo i najjednostavnijeg resenja:



***

Sabiranjem ove dve jednakosti dobija se

tj, , odakle je , tj, (posto su a i b pozitivne velicine, i zbir im je pozitivan) (1)


S druge strane, oduzimanjem (***) se dobija tj, , odakle je (2)

Paznja!
Ovde je neophodno da naglasis a>b , jer razlika dve pozitivne velicine nije obavezno pozitivna. Za b>a samo bi a i b 'zamenili uloge', tj imao bi da je
, sto se posle mnozenja sa -1 svodi na

Dakle, iz (1) i (2), dobijamo nov sistem (linearnih) jednacina:

, za , odakle je



Za b>a, bilo bi



Drzimo ti palceve za sutra!

Evo konačno sam završio kompletan zadatak, ovako izgleda





Hvala svima još jednom.

Smjenom i uvrštavanjem u jednačinu dobijamo bikvadratnu jednačinu .

Riješimo bikvadratnu jednačinu:

,

smjena:;

,
;

,
.

Odredimo :

,
,
;

,
,
.

Odredimo sada :

,
;

,
.

Dobili smo skup rješenja sistema jednačina:

.

Pošto i ne mogu biti negativni brojevi, traženi skup rješenja je:

.

Dalje ti je lako iz sinusne teoreme da odrediš i :

;
,
.