Moraš da kažeš koje oblasti ti trebaju. Uzgred, gde studiraš i šta?

Studiram informatiku na PMF-u u Novom Sadu...treba mi za predmet "Teorijski osnovi informatike"...radimo iskazni i predikatski račun...

jel moze neko da uradi u L(iskaznom racunu),probao sam sve ne znam....

Probaj da dokažeš kontrapoziciju, koja se posle primene pravila dedukcije svodi na

.

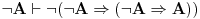
Obzirom na

(1) ,

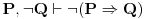
svodi se na

(2) ,
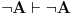
(3) .

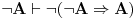
(2) je trivijalno. (3) se prema (1) svodi na (2).

Kako dokazati (1)? Pa važi

,
,

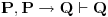
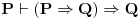
obzirom na

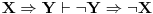
(4) , važi

,

odakle sledi (1). (4) se lako dokazuje na osnovu modus ponensa, treće aksiome i

(5) ,

odnosno po pravilu dedukcije

.

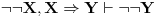
No, ovo se lako izvodi ako znamo da

i .

Primenom prve aksiome i pravila dedukcije izvodi se da važi

,

a na osnovu dvostruke primene modus ponensa i treće aksiome

,

odakle trivijalno sledi prvi deo. Na osnovu toga i pravila dedukcije je

,

pa je na osnovu modus ponensa i treće aksiome

,

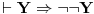
odakle sledi drugi deo.

_{[Ovu poruku je menjao Nedeljko dana 16.11.2012. u 15:38 GMT+1]}