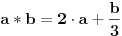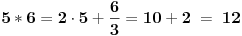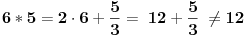[ nick2 @ 12.11.2010. 15:14 ] @
| pozdrav, kako dokazati grupoidnost na primer: skup Q a*b =2a+b/3 (gde je * bilo koji znak ), uopste kako dokazivati grupoidnosti koje nemaju odredjeni znak (da je receno da je *=+,-, onda znam) ps: zadatak je ustvari ISPITATI ALGEBARSKU STRUKTURU ali meni je problem samo dokazivanje grupoidnosti |