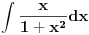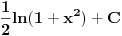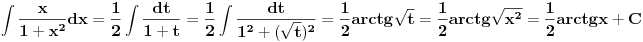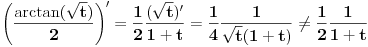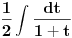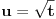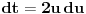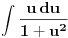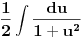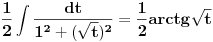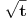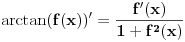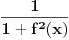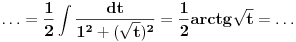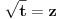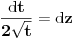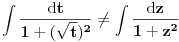Probaj da u integralu uvedeš smenu . Zbog integral se svodi na , a ne na .

Ova jednakost nije tacna... u imeniocu ti je a u brojiocu dt

Proverio sam i ja racun "otpozadi", ali mi on nije dao odgovor na pitanje gde gresim. On mi je samo rekao da gresim negde. Drugi red: ako u taj integral uvedem smenu koju predlazes dobijem pocetni problem, naravno da cu to da dobijem, time je "anulirana" smenu x^{2} = t i vratili se na pocetak.

Sta tacno nije u redu sa tom jednakoscu? Mozes li da mi napises LevaStrana[onako_kako_stoji] = TacnaDesnaStrana[onako kako ti smatras].

skontao sam u cemu je caka: smena koju nedeljko predlaze je "obavezna" ako hocu da pucam na arctg (u tom smislu jednakost koju pominje montenegr1 nije tacna, i zaista nije tacna), a kada je uradim dobijem pocetni problem, a ne arctg. Drugim recima t sustinski mora biti kvadratna funkcija ako zelim da pucam na arctg, ja sam samo kroz formalizam namestio da ona tako izgleda.

hvala.

Poenta je u tome da je , a ne .

nisam bas proradio zadatak ... ali javi mi ako parcijalnom integracijom na kraju dobijes arctg .... u stavi da je u = 1/(1+x^2) .... vjerovatno lupam i kasno je pa ne znam jesam li dobro shvatio muku ovu ... heheheh ... pozdrav

_{[Ovu poruku je menjao Maka_Madafaka dana 18.11.2010. u 05:21 GMT+1]}

Tu je greška. Ako ti je već , , onda .

Kada primenjuješ smenu, moraš da promeniš sva mesta gde se javlja stara promenljiva (tj. i njen diferencijal).