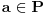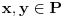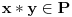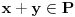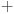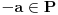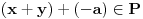U prvoj recenici postavke pise da je P polje, dakle zatvoren u odnosu na sabiranje i mnozenje, pa je na osnovu toga zatvoreno i u onosu na novodefinisane operacije

Da pise da je P za plus i mnozenje polje ali kako da odatle izvedem da je P zatvoreno za * koja je definisana kao x*y=x+y-a samo a je iz P koje je polje a i ono je proizvoljno za x+y ne znamo nista, mada sabiranjem se ostaje u istom skupu ali ovaj minus ispred a me buni, kako da znam da ovo x+y ce biti vece od a, kako to dokazati...

Ne znam šta te buni.
Za polje je potrebno da postoji inverzan element (-a) za operaciju +.
x i y su iz P, dakle bilo koja dva elementa koja pripadaju skupu P.

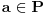
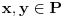
Dakle, po pretpostavci . Zatvorenost znači da kad god su mora biti i .

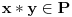
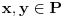
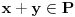
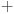
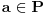
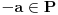
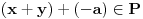
Dakle, ako su , onda mora biti jer je zatvoreno za . Ali, pošto , onda i , jer je polje, pa . Je li sada jasnije?