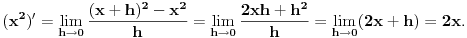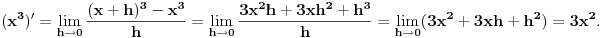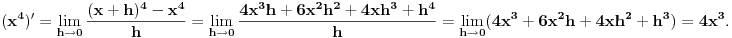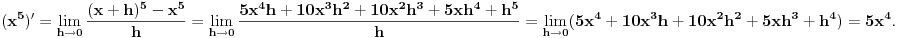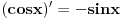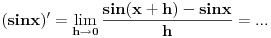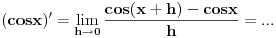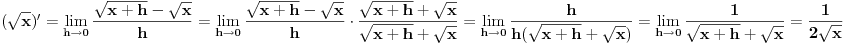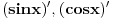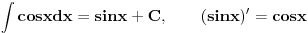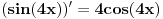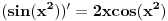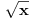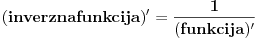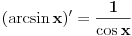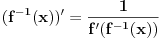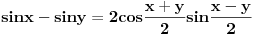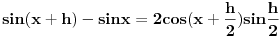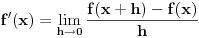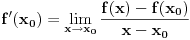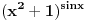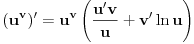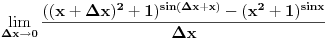|
|
[ keledelboy @ 23.11.2010. 23:00 ] @
|
| pozdrav svima. imam jedno pitanjce za koje verujem da ovde neko zna odgovor, ovako stoje stvari, u skoli kad su nas ucili da resavamo izvode i integrale nekih funkcija sve se svodilo na natezanje na tablicno resenje. znaci prepoznas koji slucaj ti je zadat i ti ga malo prekrojis navuces na neko poznato tablicno resenje. mene interesuje sta se tu desava "ispod haube" - primer izvod od x^2 = 2x , to nam je receno u tablici, moje pitanje je da li i to moze nekako da se izracuna peske, kako je neki genijalac to izracunao koji je i sastavio tu prvu tablicu. e sad ovo pitam zato sto sam SKORO siguran da postoji univerzalan sistem (algoritam)za resavanje i izvoda i integrala zato sto sam pronasao neke kalkulatore koji racunaju i izvode i integrale pisane u java ME koji rade na nekom starom krsu od telefona sto znaci da algoritam ne moze biti preterano komplikovan, nekada sam video delimican source code u C-u i nije delovalo toliko strasno i komplikovano uglavnom algoritam koristi primitivnu matematiku bez nekih slozenih funkcija, operacija, limesa, i ostalog, i na kraju da li je neko voljan da pokusa da mi ovo objasni ili da me uputi negde gde bi mogao nesto procitati o ovome po mogucstvu na nekom balkanskom jeziku, ako nesto nije jasno u ovom postu razjasnicu nekim narednim postom.
HVALA UNAPRED |
[ Nedeljko @ 23.11.2010. 23:40 ] @
Izvod od  po definiciji:
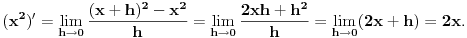
Drugo, Diferencirati je lako, ali integraliti je teško. Za izvode postoji algoritam, ne previše komplikovan, a što se integraljenja tiče, postoji algoritam i za to, ali jako komplikovan i zasniva se na jako debeloj teoriji.
[Ovu poruku je menjao Nedeljko dana 24.11.2010. u 09:59 GMT+1][ atomant @ 23.11.2010. 23:53 ] @
Samo, u poslednjem limesu h tezi nuli, ne x.
[ miki069 @ 24.11.2010. 00:07 ] @
[ Kolins Balaban @ 24.11.2010. 06:27 ] @
ama neka se prihvati udzbenika za IV razred srednje skole, tu mu ima objasnjena procedura, i detaljno je pokazano kako se dobijaju tablicni izvodi. i u svakom udzbeniku za I god fakulteta ima objasnjena ista stvar....
[ keledelboy @ 24.11.2010. 12:49 ] @
nedeljko i miki069 hvala na pomoci ovo sad deluje mnogo jasnije, samo ovo je za konkretan primer prvog tablicnog izvoda, da li mozete da mi pokazete univerzalni algoritam za resavanje izvoda ovako u matematickom obliku ili u nekom programskom obliku, a ako mi to bude poslo za rukom probacemo i sa integralima.
kolins balaban hvala i tebi na odgovoru ako kojim slucajem imas taj udzbenik iz IV razreda gimnazije da li bi mogao da mi skeniras taj univerzalni postupak za resavanje integrala i izvoda zato sto nisam u prilici da ga nabavim, a prvi razredi fakulteta bar u skorije vreme imaju samo objasnjenje sta je izvod i integral i to prilicno skromno objasnjenje i kako se navlaci na tablicu, sto opet meni nije zanimljivo zato sto sam to u velikoj meri savladao, zanimaju me samo ta dva univerzalna algoritma za resavanje izvoda i integrala u matematickom ili programskom obliku
hvala jos jednom za angazovanje.
[ petarm @ 24.11.2010. 14:51 ] @
Probaj sam da izguras npr.

i
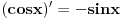
Znaci krenes isto
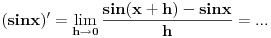
i
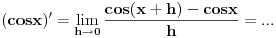
Koristi adicione formule!
Evo ti npr. koren
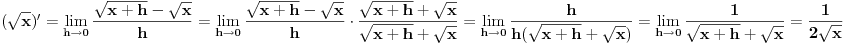
To ti je postupak! Ne znam sta drugo trazis?
[ Cabo @ 24.11.2010. 15:56 ] @
Il' je loš profan, il' neko ne pazi na času...  [ petarm @ 24.11.2010. 16:16 ] @
Citat: keledelboy: pozdrav svima. imam jedno pitanjce za koje verujem da ovde neko zna odgovor, ovako stoje stvari, u skoli kad su nas ucili da resavamo izvode i integrale nekih funkcija sve se svodilo na natezanje na tablicno resenje. znaci prepoznas koji slucaj ti je zadat i ti ga malo prekrojis navuces na neko poznato tablicno resenje. mene interesuje sta se tu desava "ispod haube" - primer izvod od x^2 = 2x , to nam je receno u tablici, moje pitanje je da li i to moze nekako da se izracuna peske, kako je neki genijalac to izracunao koji je i sastavio tu prvu tablicu. e sad ovo pitam zato sto sam SKORO siguran da postoji univerzalan sistem (algoritam)za resavanje i izvoda i integrala zato sto sam pronasao neke kalkulatore koji racunaju i izvode i integrale pisane u java ME koji rade na nekom starom krsu od telefona sto znaci da algoritam ne moze biti preterano komplikovan, nekada sam video delimican source code u C-u i nije delovalo toliko strasno i komplikovano uglavnom algoritam koristi primitivnu matematiku bez nekih slozenih funkcija, operacija, limesa, i ostalog, i na kraju da li je neko voljan da pokusa da mi ovo objasni ili da me uputi negde gde bi mogao nesto procitati o ovome po mogucstvu na nekom balkanskom jeziku, ako nesto nije jasno u ovom postu razjasnicu nekim narednim postom.
HVALA UNAPRED
Koju ides srednju skolu i ko ti predaje matematiku? [ keledelboy @ 24.11.2010. 21:42 ] @
petarm hvala lepo to je to sto sam trazio sad cu malo da se zabavljam i provezbam izvode pa cu onda da potrazim i za integrale ili ako imas odmah resenje postavi ga pa cu se zezati sa tim kasnije kad ovo prvo provezbam, srednju skolu sam zavrsio i sad radim neki bezveze posao i nisam profa, ovo zelim da znam iskljucivo radi sebe.
hvala svima na angazovanju i zamolio bih vas da mi postavite isto ovo za integrale, ako je to moguce da ne bih morao opet posle nekog vremena da otvaram novu temu
hvala jos jednom
[ petarm @ 24.11.2010. 22:26 ] @
Ok! Ne postoji ovako nesto za integrale. Jesi li isterao 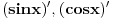 ili pokusao da isteras? Pitam ako si negde zapeo da ti damo neki hint? [ keledelboy @ 24.11.2010. 22:41 ] @
uspeo sam da isteram jasan mi je sablon i svidja mi se sto nije previse komplikovan, hvala puno na pomoci, a sta je sa integralima nema uopste sablona ili je komplikovan ili postoji vise sablona, gore je nedeljko pomenuo da postoji nesto i za integrale (kako bi ga inace kompjuter racunao i los mobilni telefon) ali dosta slozenije koliko sam ga razumeo, da li taj komplikovan nacin mozes da postavis ili da me uputis na njega ili bilo sta da mi pokazes da me uvedes u tu problematiku.
[ rikelme @ 24.11.2010. 22:48 ] @
Pridružujem se savetima vezanih za ručno integraljenje pomoću "univerzalne" formule. Isečak iz opisa funkcije integraljenja iz Wolfram Mathematica programa:
Citat:
Mathematica's Integrate function represents the fruits of a huge amount of mathematical and computational research.
It doesn't do integrals the way people do. Instead, it uses powerful, general algorithms that often involve very sophisticated
math. There are a couple of approaches that it most commonly takes. One involves working out the general form for an
integral, then differentiating this form and solving equations to match up undetermined symbolic parameters. Even for quite
simple integrands, the equations generated in this way can be highly complex and require Mathematica's strong algebraic
computation capabilities to solve. Another approach that Mathematica uses in working out integrals is to convert them to
generalized hypergeometric functions, then use collections of relations about these highly general mathematical functions.
Inače, većina kalkulatora i software-a koriste numeričke metode integraljenja, diferenciranja... [ petarm @ 24.11.2010. 23:00 ] @
Citat: keledelboy: uspeo sam da isteram jasan mi je sablon i svidja mi se sto nije previse komplikovan, hvala puno na pomoci, a sta je sa integralima nema uopste sablona ili je komplikovan ili postoji vise sablona, gore je nedeljko pomenuo da postoji nesto i za integrale (kako bi ga inace kompjuter racunao i los mobilni telefon) ali dosta slozenije koliko sam ga razumeo, da li taj komplikovan nacin mozes da postavis ili da me uputis na njega ili bilo sta da mi pokazes da me uvedes u tu problematiku.
Ne mozes naci integral od ma kakve funkcije analiticki. Cesto se koriste numericki postupci. Inace postoji mnogo postupaka za integraljenje smena, parcijalna integracija, integral binomnog diferencijala, Ojlerove smene...
E sad ako te zanimaju tablicni, tu nije problem
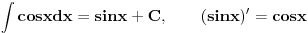
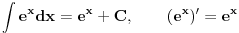
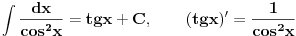
...
Shvatas ideju! Moras nabaviti neki udzbenik. Npr. udzbenik iz matematike za IV gimnazije pa procitati i pitati sta ti nije jasno! [ Nedeljko @ 24.11.2010. 23:53 ] @
Citat: petarm: Ne mozes naci integral od ma kakve funkcije analiticki.
Može, ali je postupak samo za eksperte u toj oblasti. Naravno, nije integral svake elementarne funkcije elementarna funkcija, ali ako se skup osnovnih funkcija proširi, dobija se zatvoren skup funkcija za integraciju i onda može. [ miki069 @ 25.11.2010. 00:56 ] @
Ako si uradio:
 ,
Uradi obavezno i:
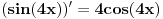 i
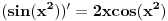
Time će ti postati jasan izvod složene funkcije.
Petar ti je pokazao izvod po definiciji od 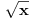 .
Izvode od ln(x), arcsin(x) i arccos(x) uradi preko Teoreme o izvodu inverzne funkcije.
Direktna izrada je komplikovana za ln(x), a za arkus funkcije ja i ne znam izradu bez Teoreme.
Preko te Teoreme možeš da uradiš i izvod od 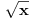 .
Teorema:
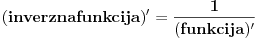 [Ovu poruku je menjao miki069 dana 25.11.2010. u 02:06 GMT+1]
[Ovu poruku je menjao miki069 dana 25.11.2010. u 02:06 GMT+1][ Nedeljko @ 25.11.2010. 09:03 ] @
Pomisliće neko da je 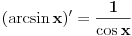 . Zapravo je
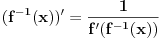 .
[ keledelboy @ 25.11.2010. 09:36 ] @
nema sanse te slozene funkcije da resim, moram opet da vidim neki primer, ne umem da postavim, potrazicu taj udzbenik iz matematike za IV gimnazije pa cu pogledati i javiti se ako mi nesto ne bude bilo jasno posle toga. nedeljko i miki069 da li mozete da me uputite gde ima ovo isto o integralima knjiga, sajt ili nesto trece.
hvala svima na vremenu i angazovanju
[ different @ 25.11.2010. 10:26 ] @
Drugo, Diferencirati je lako, ali integraliti je teško. Za izvode postoji algoritam, ne previše komplikovan, a što se integraljenja tiče, postoji algoritam i za to, ali jako komplikovan i zasniva se na jako debeloj teoriji
Nedjeljko,
pokusavam pronaci literauru o integraljenju po definiciji al mi ne ide od ruke,mozes li jedan primjer uraditi kao za racunanje izvoda ili ako mozes neku literaturu preporucita,zaista me to interesuje.
[ 3MAJ86 @ 25.11.2010. 10:32 ] @
Nemoj se uvrediti što ovo pitam, ali znaš li uopšte šta je izvod, i kako se računa u opštem slučaju?
I nisi odgovorio na pitanje, u koju školu ideš i ko ti predaje matematiku?
Ispravi me ako grešim, ali meni se čini da ti želiš da nađeš način kako preko mobilnog da rešavaš izvode i integrale na kontrolnim/pismenim vežbama.
[ Nedeljko @ 25.11.2010. 11:05 ] @
Citat: different: pokusavam pronaci literauru o integraljenju po definiciji al mi ne ide od ruke,mozes li jedan primjer uraditi kao za racunanje izvoda ili ako mozes neku literaturu preporucita,zaista me to interesuje.
Ja taj kompletan algoritam za integraljenje ne znam, samo znam da postoji i da ga koristi volframov integrator. Znam i da je jako složen i da ne bi mogao da ga prati prosečan diplomirani matematičar bez ozbiljnih priprema. [ Cabo @ 25.11.2010. 11:06 ] @
@pokretač teme: Možeš da upotrebiš bilo koji udžbenik za gimnaziju ili tehnički fakultet.
Neki od dobrih udžbenika za fakultete su, npr. „Analiza I“ od Zorana Kadelburga i „Kurs diferencijalnog i integralnog računa“ („  “) od Grigorija Mihajloviča Fihtengoljca (  ) [ miki069 @ 25.11.2010. 14:43 ] @
Keledeboy: napiši kako si uradio izvod sinx i dokle dođeš u izvodu od sin(4x).
[ R A V E N @ 25.11.2010. 19:02 ] @
Citat: different: Drugo, Diferencirati je lako, ali integraliti je teško. Za izvode postoji algoritam, ne previše komplikovan, a što se integraljenja tiče, postoji algoritam i za to, ali jako komplikovan i zasniva se na jako debeloj teoriji
Nedjeljko,
pokusavam pronaci literauru o integraljenju po definiciji al mi ne ide od ruke,mozes li jedan primjer uraditi kao za racunanje izvoda ili ako mozes neku literaturu preporucita,zaista me to interesuje.
Šta mislite, koliko će vam trebati vremena da to s razumijevanjem savladate? Pitanje i za autora teme.
[Ovu poruku je menjao R A V E N dana 25.11.2010. u 20:12 GMT+1][ keledelboy @ 25.11.2010. 19:42 ] @
3MAJ86 srednju skolu sam zavrsio i vise se ne skolujem zelim samo da pokusam sa ovim da izadjem na kraj da bi se lepse osecao da mi treba za muljanje to bi rekao i to vec imam za mobilni telefon racuna sve osim neodredjenih integrala, racuna definisane integrale, izvode, matrice, ........
R A V E N trebace mi verovatno mnogo vremena koje imam i zelim da ga potrosim na ovo a usput imam i strpljenja
miki069 kod izvoda sin(4x) ne dodjem nigde ne znam da postavim limes probao sam ovako ali ne dobijem dobro resenje lim h->0 = (sin(4x+h)-sin(4x))/h
onaj drugi tvoj primer postavim lim h->0 = (sin(x+h)^2)-(sin(x^2))/h
i opet ne dobijem dobro resenje jedino ako zeznem negde u racunanju.
[ keledelboy @ 25.11.2010. 20:43 ] @
http://en.wikipedia.org/wiki/N...rdinary_differential_equations
ovde ima objasnjenje za ovaj sablon sto ste mi pokazali i postoje jos neke mogucnosti jedino sto je na engleskom jbg
[ petarm @ 26.11.2010. 00:07 ] @
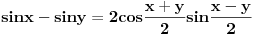
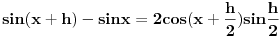
Pomaze li ovo? [ blackholemix @ 26.11.2010. 00:10 ] @
Za izvod je lako, jer je izvod jedinstven, koristi se skup pravila pomocu kojih se dobija izvod bilo koje funkcije. Neke funkcije nisu diferencijabilne u nekoj tacki. Ili vise tacaka, ali vecina je svuda diferencijabilna, dok sa druge strane postoje mnoge funkcije ciji neodredjeni integral ne moze da se odredi, tj. nemaju primitivnu funkciju.
Algoritam ili postupak za nalazenje izvoda je:
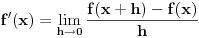
ili, mozda i lepse
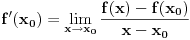
Integral se definise kao primitivna funkcija F(x) za funkciju f(x) i ako vazi F'(x)=f(x) i jos neke stvari oko definisanosti. Takodje integrala ima citava klasa, nije jedinstven. Zato se dodaje ono C po ruskoj skoli, mada Amerikanci to ne pisu i za njih se trazi samo jedna primitivna funkcija.
Jasno je da sve ovo dovodi do toga da svako razume da je nalazenje integrala daleko komplikovanije od nalazenja izvoda. Najbolji softverski paket koji izvrsava oba operatora je Malpe! Da ovo oko intergala uopste nije jednostavno pokazuje MuPAD, nemacka alternativa za Maple, koja postoji i u okviru Matlaba. Nedavno sam ga malo cackao, i nasao toliko mana, integrala koje ja usmeno resavam, a on cak ne ume. Naravno Maple bi ipak to resio. Zato ako mislite da cete u nekom programskom jeziku da napisete program koji ce resavati integrale, varate se, necete. [ miki069 @ 26.11.2010. 00:38 ] @
Koje "pravilo" izvoda reguliše izvod funkcije:
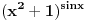 ?
Nije baš tako lako ni izvode formalizovati, ali je moguće.
Za neodređene integrale se divim pokušaju.
[ keledelboy @ 26.11.2010. 01:10 ] @
hvala svima na angazovanju puno ste mi pomogli, sad imam materijala da se zabavljam sa ovim stvarima, ako neko naidje ko ima isto ovo za integrale bilo bi lepo da to podeli sa nama radoznalima.
[ 3MAJ86 @ 26.11.2010. 08:49 ] @
Ok, izvinjavam se onda na pogrešnoj pretpostavci.
Program za rešavanje integrala na telefonu... teško :)
Ako želiš mogu da ti preporučim jednu skripticu (ili kako već da je nazovem) gde imaju urađeni tablični integrali plus su objašnjeni neki slučajevi koji se često pojavljuju i neke 'fore' kako se dolazi do istih. Ne znam koliko ti je bitno i u koje svrhe želiš da naučiš da to radiš, ali ako želiš da naučiš izvode i integrale sa razumevanjem pogledaj malo teoriju. Zaista nije teško, i lako je razumljivo.
Takođe bih preporučio Kadelburgovu Analizu 1 koju je gore neko već spomenuo.
[ Nedeljko @ 26.11.2010. 09:35 ] @
Citat: miki069: Koje "pravilo" izvoda reguliše izvod funkcije:
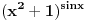 ? 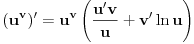 . [ Fermion @ 26.11.2010. 09:54 ] @
Da, ali u ovom primeru nije trivijalno naći izvod po definiciji...
[ Nedeljko @ 26.11.2010. 11:37 ] @
To nije bilo pitanje.
[ Fermion @ 26.11.2010. 12:23 ] @
Pa koliko sam ja shvatio temu ona se baš i odnosi na nalaženje izvoda po definiciji, ja se izvinjavam ako sam pogrešio.
Ovde imamo sasvim netrivijalan limes:
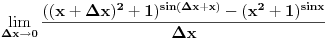 [ since1986BC @ 26.11.2010. 15:37 ] @
Za pokretaca teme: De uvedi malo pravopisa u svoje postove. Ja se ubi da rastumacim sta "govoris".
Budi malo fer prema ljudima koji zele ili ti vec pomazu.
Usput, mozda link bude od koristi.
http://www.matematiranje.com/4godina.html
[ keledelboy @ 26.11.2010. 19:03 ] @
izvinjavam se zbog pravopisa nespretan sam jako sa tastaturom, nemoj te mi zameriti trudim sa koliko mogu. hvala za link
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|