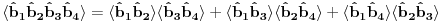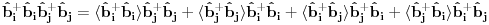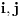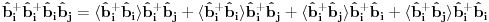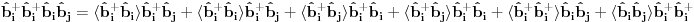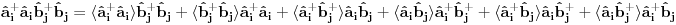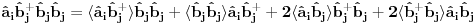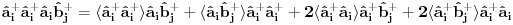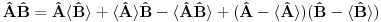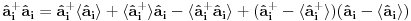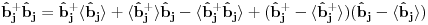[ petarm @ 24.11.2010. 13:48 ] @
|
[ NicholasMetropolis @ 25.11.2010. 10:52 ] @
Citat: petarm: 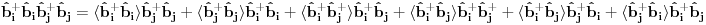 ? ?Zato što je član 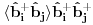 očigledno pogrešan i zato što su očekivane vrednosti oblika očigledno pogrešan i zato što su očekivane vrednosti oblika  i i 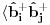 jednake nuli. Zašto? Zato što je očekivana vrednost operatora, u svojstvenom bazisu Hamiltonijana jednake nuli. Zašto? Zato što je očekivana vrednost operatora, u svojstvenom bazisu Hamiltonijana 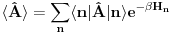 što znači da operator što znači da operator 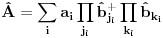 mora imati jednak broj kreacionih i anihilacionih operatora da bi mora imati jednak broj kreacionih i anihilacionih operatora da bi 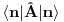 bilo raziličito od nule. bilo raziličito od nule.Slično i za drugi primer koji si naveo. I da, ovo se ne zove self consistent spin wave theory. Ovo je obična matematika. Self consistent spin wave theory je metod za rešavanje Hajzenbergovog modela. Pogledaj malo po netu. Imaš brdo referenci. [ petarm @ 25.11.2010. 13:15 ] @
Pre svega hvala na odgovoru. Iskreno ne bih bio zbunjen s ovim da kod antiferomagneta ne postoje dekuplovanja sledecih operatora:
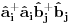 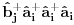  Ovo treba dekuplovati.  su Boze operatori. Deluju u razlicitim podresetkama. Ocito u drugom i trecem slucaju imam proizvod tri kreaciona, odnosno tri anihilaciona operatora respektivno. Naravno vazi su Boze operatori. Deluju u razlicitim podresetkama. Ocito u drugom i trecem slucaju imam proizvod tri kreaciona, odnosno tri anihilaciona operatora respektivno. Naravno vazi  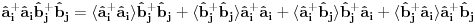 Ali kako ovo dekuplovati? 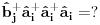 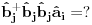 [Ovu poruku je menjao petarm dana 25.11.2010. u 15:06 GMT+1] [Ovu poruku je menjao petarm dana 25.11.2010. u 15:08 GMT+1] [ NicholasMetropolis @ 26.11.2010. 13:04 ] @
Citat: Nisam siguran da je ovo tačno, zato što ako su 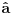 i i 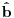 anihilacioni operatori za različite vrste čestica, onda imaš da je anihilacioni operatori za različite vrste čestica, onda imaš da je 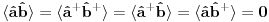 Na osnovu ovoga mislim da bi trebali da imamo:  i i 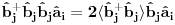 E da, i zašto se ovo zove self-consistent spin wave theory: Kada npr imaš Hajzenbergov hamiltonijan 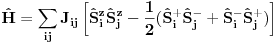 , nalaženje očekivane vrednosti bilo kog operatora podrazumeva izračunavanje , nalaženje očekivane vrednosti bilo kog operatora podrazumeva izračunavanje 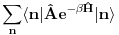 (1) (1)što je u opštem slučaju nemoguće uraditi analitički zbog prisustva eksponencijalne funkcije. Prva stvar je da mapiraš operatora spina na operatore druge kvantizacije. To možeš da uradiš pomoću Holšten-Primakov, Dajson Maleev ili nekih drugih transformacija. Pošto tada u razvoju eksponencijalne funkcije imaš proizvode operatora 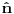 , ,  i i 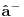 , problem pojednostavljuješ tako što proizvod većeg broja operatora svedeš na sumu proizvoda sa manjim brojem operatora (ono dekuplovanje koje si ti radio) tako što određeni broj operatora zameniš njihovim srednjim vrednostima. Naravno, ovde se vrtiš u krug, pošto, da bi izračunao srednju vrednost moraš biti u stanju da izračunaš (1), a ovu aproksimaciju smo uveli da bismo upravo izračunali (1). , problem pojednostavljuješ tako što proizvod većeg broja operatora svedeš na sumu proizvoda sa manjim brojem operatora (ono dekuplovanje koje si ti radio) tako što određeni broj operatora zameniš njihovim srednjim vrednostima. Naravno, ovde se vrtiš u krug, pošto, da bi izračunao srednju vrednost moraš biti u stanju da izračunaš (1), a ovu aproksimaciju smo uveli da bismo upravo izračunali (1). Kako se izlazi iz ovog začaranog kruga? Tako što pretpostavimo da je problem samokonzistentan. Tj. pretpostavimo početne očekivane vrednosti, ubacimo ih u (1) i izračunamo nove očekivane vrednosti pa onda ceo proces ponavljamo. Ako je problem samokonzistentan, očekujemo da će, kako ovaj iterativni proces napreduje, očekivane vrednosti početi da konvergiraju ka tačnim vrednostima. Naravno, ovo je samo grubi opis modela. Sve to ide malo finije, pošto se ceo problem analitički svede na par relativno jednostavnih samokonzistentih jednačina koje možeš numerički da rešiš. Evo, pogledaj npr Phys. Rev. B 60, 1082–1099 (1999) (preprint: http://arxiv.org/abs/cond-mat/9901027) - jedna od prvih referenci kada potražiš "self consistent spin wave theory na Google Scholar". Tu imaš ceo postupak za slojevite Hajzenbergove magnete. [ petarm @ 26.11.2010. 18:22 ] @
Citat: NicholasMetropolis: Nisam siguran da je ovo tačno, zato što ako su 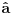 i i 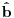 anihilacioni operatori za različite vrste čestica anihilacioni operatori za različite vrste česticaOvaj boldovan deo mi je malo zbunjuce formulisan. U kom smislu razlicite vrste cestica? Ja to posmatram kao dve podresetke. U jednom podreseci imam up spinove, a drugoj down spinove. E sad kad sa tih spinskih predjem na bozonske operatore, u jednoj podreseci imacu 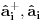 , a u drugoj , a u drugoj  . Pa me ovaj termin razlicite vrste cestica malko zbunjuje. . Pa me ovaj termin razlicite vrste cestica malko zbunjuje. Citat: NicholasMetropolis: Nisam siguran da je ovo tačno, zato što ako su 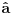 i i 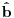 anihilacioni operatori za različite vrste čestica, onda imaš da je anihilacioni operatori za različite vrste čestica, onda imaš da je 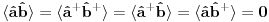 Na osnovu ovoga mislim da bi trebali da imamo:  i i 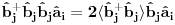 Ako vazi ovo sto si napisao, a trebalo bi da vazi imamo: 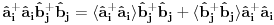 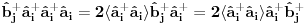 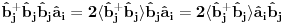 E sad da li se nesto menja ako imamo 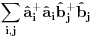  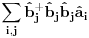 ? [ NicholasMetropolis @ 26.11.2010. 21:37 ] @
Citat: petarm: Ovaj boldovan deo mi je malo zbunjuce formulisan. U kom smislu razlicite vrste cestica? Ja to posmatram kao dve podresetke. U jednom podreseci imam up spinove, a drugoj down spinove. E sad kad sa tih spinskih predjem na bozonske operatore, u jednoj podreseci imacu 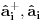 , a u drugoj , a u drugoj  . Pa me ovaj termin razlicite vrste cestica malko zbunjuje. . Pa me ovaj termin razlicite vrste cestica malko zbunjuje. Različite čestice u smislu da su prostori u kojima deluju ovi operatori različiti. Svaka podrešetka ima prostor stanja za sebe. Citat: Ne vidim zašto bi se menjalo. Sve je u suštini isto, samo moraš malo više da pišeš pošto imaš zbir gomile članova gde na svaki član moraš da primeniš dekuplovanje. [ petarm @ 27.11.2010. 08:19 ] @
Na jednom forumu dobio sam sledeci odgovor
This is a method of mean field theory. In Hartree-Fock approximation, there is only <a+a>, but no <a+a+> or <aa>. because the latter is zero. But, for some condensed system, such as Lasers and Superconductors, the double creation and double destruction process is important. In the mean field theory, one can also average the operators, just like <a+a+> and <aa>. In that time, they are not zero. [ NicholasMetropolis @ 27.11.2010. 10:15 ] @
Citat: petarm: Na jednom forumu dobio sam sledeci odgovor This is a method of mean field theory. In Hartree-Fock approximation, there is only <a+a>, but no <a+a+> or <aa>. because the latter is zero. But, for some condensed system, such as Lasers and Superconductors, the double creation and double destruction process is important. In the mean field theory, one can also average the operators, just like <a+a+> and <aa>. In that time, they are not zero. Srednje vrednosti za dupli kreacioni ili anihilacioni operator ne moraju biti nula kada sistem nema ravnotežnu statistiku (tj. kada srednju vrednost ne možeš da izračunaš u nekom od ravnotežnih ansambala - ja sam gore koristio kanonski) što je npr. slučaj sa laserima. [ NicholasMetropolis @ 27.11.2010. 10:59 ] @
Citat: petarm: Uopsteno dekuplovanje bi bilo... Uopšteno, mogao bi da uzmeš i očekivane vrednosti tri ili četiri operatora. Poenta je da ovo radiš da bi pojednostavio problem u meri kojoj je tebi to potrebno. Ako se igraš sa Hajzenbergovim modelom (pretpostavljam da ti je to namera) toliko uopštenje ti nije potrebno zato što posmatraš sistem u ravnoteži (osim ako ti baš nisu zanimljivi prelazni režimi u sistemu) pa možeš da koristiš neki ravnotežni ansambl. [ petarm @ 27.11.2010. 12:05 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|