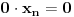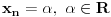[ R A V E N @ 26.11.2010. 01:26 ] @
| Ako imamo nehomogeni sistem linearnih jednačina sa jednom nepoznatom više od broja jednačina i ako na taj sistem primjenimo Gaussovu eliminaciju da bi ga riješili, dobivamo u zadnjoj jednačini dvije nepoznate (što, pretpostavljam, važi u opštem slučaju za ovakve sisteme) i ne možemo dalje poništavati nepoznate. Nakon toga u toj zadnjoj jednačini samo jednu nepoznatu izrazimo preko druge i tako izrazimo sve nepoznate. Da ili ne? |
 Tema se može obrisati.
Tema se može obrisati.