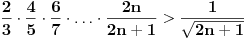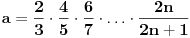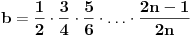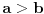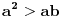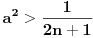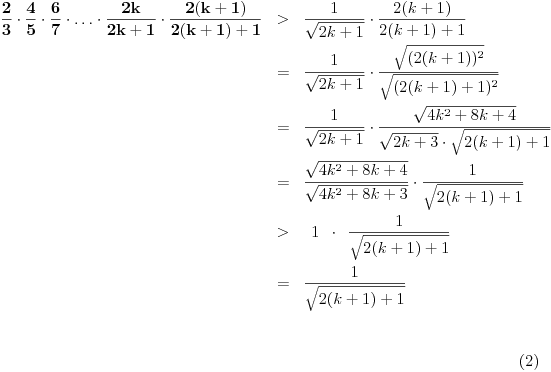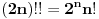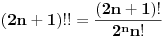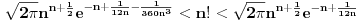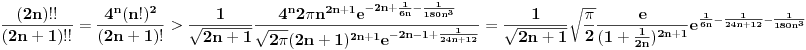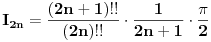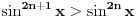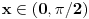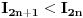[ Fermion @ 27.11.2010. 18:00 ] @
|
[ Fermion @ 28.11.2010. 11:16 ] @
Hvala na odgovorima.
Moram reći da se matematička indukcija pokazala kao jako efektivna u ovakvim zadacima. Nastavio sam da tražim još rešenja kod ovog zadatka i došao do novog pitanja. Da li se od proizvoda može napraviti opšti oblik, kao što može od sume? Recimo kao što je 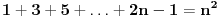 slično za proizvod u zadatku? slično za proizvod u zadatku?Ideja bi bila u tome da se nađe taj proizvod u opštem slučaju, i ako mu je vrednost  da se pokaže da je za svaki prirodan broj n ispunjeno: da se pokaže da je za svaki prirodan broj n ispunjeno: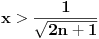 [ Nedeljko @ 28.11.2010. 14:02 ] @
[ Fermion @ 28.11.2010. 14:25 ] @
[ Nedeljko @ 28.11.2010. 16:01 ] @
[ Nedeljko @ 29.11.2010. 09:13 ] @
Stirlingova formula.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|