|
|
[ miki208 @ 28.11.2010. 20:43 ] @
|
| Pozz svima.Cilj ove teme je da zajedno postavljamo i resavamo zadatke.Onaj ko resi prethodni zadatak ,postavlja novi itd. :D
Milsim da ako svi uloze trud da ce biti zabavno.
Evo da krenemo:
Napraviti program koji od korisnika trazi unos stranica a i b jednog pravougaonika,a program treba da izracuna obim i povrsinu,a zatim da ispise te podatke. |
[ X Files @ 29.11.2010. 06:10 ] @
A ja mislio da je cilj ove teme da se tebi uradi domaci zadatak.
[ mihojla @ 29.11.2010. 06:32 ] @
evo:  Code:
#!/usr/bin/perl
use strict;
unless(@ARGV>1){print "unesi stranice kvadrata: $0 a b\n";exit}
my $a=shift(@ARGV);
my $b=shift(@ARGV);
print 'P='.$a*$b.', O='.2*($a+$b)."\n"; [ Nedeljko @ 29.11.2010. 09:25 ] @
Nisi završio posao. Treba da postaviš novi zadatak.
[ miki208 @ 29.11.2010. 20:29 ] @
Hehe,nije domaci,nego sam postavio ovu temu jer nigde na internetu ne mogu da pronadjem neke dobre zadatke iz programiranja pa sam odlucio da se ovde svi pomucimo malo xD.Hteo sam da zadaci krenu od onih laksih pa da svaki novi zadatak bude tezi.
[ Mihajlo Cvetanović @ 30.11.2010. 09:57 ] @
Ako te interesuju ne-trivijalni problemi onda poseti http://uva.onlinejudge.org/ . Tu imaš obilje zadataka sa svih ACM takmičenja do sada, i sistem za proveru rešenja (server kompajlira tvoj sors i testira izvršavanje preko sopstvenih testnih primera). Ovaj sajt će te okupirati bar godinu dana (ako si stvarno dobar). [ mihojla @ 30.11.2010. 11:53 ] @
Citat: Nisi završio posao. Treba da postaviš novi zadatak. Program koji ce upisati brojeve od 1-125 u kocku 5x5x5 tako da zbir u svakoj koloni i svakom redu bude jednak.
Ignorišite ovaj zadatak jer ni ja nisam uspeo da ga rešim.
[Ovu poruku je menjao mihojla dana 01.12.2010. u 09:51 GMT+1][ itf @ 01.12.2010. 09:24 ] @
Evo jednog tek toliko za zagrijavanje :)
Neka u programu postoji 1000 funkcija koje se sve redom zovu
void f1();
void f2();
...
void f1000();
Napiši program koji slučajnim odabirom poziva jednu od njih. Tijela funkcija su nebitna.
[ mmix @ 01.12.2010. 10:49 ] @
moze ako su funkcije dll exported 
Code (cpp):
extern "C" {
__declspec(dllexport) char* f1() { return "F1"; }
...
__declspec(dllexport) char* f999() { return "F999"; }
__declspec(dllexport) char* f1000() { return "F1000"; }
}
typedef char* (*RandomFunc)();
int _tmain(int argc, _TCHAR* argv[])
{
unsigned int r;
char fname[5];
rand_s(&r);
r = (r % 999) + 1;
sprintf_s(fname, "f%i", r);
HMODULE hm = GetModuleHandleA("Random1000.exe");
RandomFunc f = (RandomFunc)GetProcAddress(hm, fname);
DWORD xx = GetLastError();
std::cout << f();
return 0;
}
moze i iz current PIDa da se izvuce process exe, da bude bas "univerzalno"  [ Mihajlo Cvetanović @ 01.12.2010. 10:53 ] @
Može i ako funkcije nisu eksportovane, samo napraviš niz od 100 pointera na funkcije, i u 100 linija koda ga popuniš.
[ mmix @ 01.12.2010. 11:06 ] @
Tja, nije to to  sta da vam radim kad nemate refleksiju  Inace, ima 1000 funkcija, znaci 1000 dodatnih linija koda. [ Strojko @ 01.12.2010. 11:15 ] @
Zar je ovo C/C++ code:
#!/usr/bin/perl
use strict;
unless(@ARGV>1){print "unesi stranice kvadrata: $0 a b\n";exit}
my $a=shift(@ARGV);
my $b=shift(@ARGV);
print 'P='.$a*$b.', O='.2*($a+$b)."\n";
Mislio sam da znam bar osnovnu sintaksu C/C++ !!!
U čemu je stvar, ne pratim toliko Standard ali sumnjam da se toliko promenilo? Je li ovo Perl?
Evo jedan sa školskog takmičenja:
Dat je niz A od N prirodnih brojeva (N<=500) . Napisati program kojim se ispisuje indeks onog elementa u nizu
A za koji je zbir elemenata niza koji stoje pre tog elementa najmanje razlikuje od zbira elemenata niza koji stoje posle njega.
Moja verzija rešenja je ( indeks koji se ispisuje je matematički, veći je za 1 od indeksa u C++ nizu jer ne počinje od 0 ):
Code (cpp):#include<iostream>
#include<cmath>
using namespace std;
int main(){
int a[500],razlika[500],N,i,j,k,m,s,min,leva,desna;
cout<<"Unesite broj elemenata niza (manji od 500): ";
cin>>N;
for(i=0;i<N;i++){
cout<<"a["<<i<<"]= ";
cin>>a[i];}
razlika[0]=10000;
razlika[N-1]=10000;
for(i=1;i<N-1;i++){
leva=0;
desna=0;
for(j=0;j<i;j++){
leva += a[j];}
for(m=i+1;m<N;m++){
desna += a[m];}
razlika[i]=abs(desna - leva);}
for(s=0;s<N;s++){ //samo ispisuje niz razlika[],provere radi
cout<<"razlika["<<s<<"]= "<<razlika[s]<<endl;}
min = razlika[1];
for(i=0;i<N;i++){
if(razlika[i]< min){
min = razlika[i];}}
for(i=0;i<N;i++){
if( razlika[i]==min){k=i+1;} }
cout<<"Broj indeksa je: "<<k<<endl;
system("PAUSE");
return 0;
}
Ima li neko savet za optimizaciju, osim onog vezanog za veliki broj promenljivih, to sam namerno ubacio?
[Ovu poruku je menjao mmix dana 01.12.2010. u 12:28 GMT+1][ Nedeljko @ 01.12.2010. 11:24 ] @
Slažem se sa Mihajlom Cvetanovićem. Ako je skup funkcija fiksan, onda se radi tako. Nema potrebe za refleksijom. Inače, tih 1000 linija koda je lako mašinski generisati.
Code:
// ...
void f1() {
cout << 1 << endl;
}
void f2() {
cout << 2 << endl;
}
// ...
void f1000() {
cout << 1000 << endl;
}
typedef void (*Function)();
Function func[1000] = {
f1,
f2,
// ...
f1000
};
// ...
func[rand()%1000]();
// ...
[ mmix @ 01.12.2010. 11:28 ] @
Jak vam onda problem, to i pocetnici umeju :)
[ Nedeljko @ 01.12.2010. 11:40 ] @
@Strojko
Code:
#include <iostream>
#include <cstdlib>
using namespace std;
int a[501];
long long suma = 0;
int main(int argc, char *argv[]) {
a[0] = 0;
for (int i = 1; i <= 500; ++i) {
cout << i << ". " << flush;
cin >> a[i];
suma += a[i];
}
long long int razlika = -suma;
long long int minimum = abs(razlika);
int indeks = 0;
for (int i = 1; i <= 500; ++i) {
razlika += a[i-1] + a[i];
if (abs(razlika) <= minimum) {
minimum = abs(razlika);
indeks = i;
}
}
cout << indeks << endl;
return EXIT_SUCCESS;
}
[ Nedeljko @ 01.12.2010. 11:45 ] @
Citat: mmix: Jak vam onda problem, to i pocetnici umeju :)
Pa, dobro, imaš i jači, pa se pokaži
Citat: mihojla: Program koji ce upisati brojeve od 1-125 u kocku 5x5x5 tako da zbir u svakoj koloni i svakom redu bude jednak. [ Strojko @ 01.12.2010. 11:48 ] @
Hvala Nedeljko.
[ jzarko @ 01.12.2010. 13:32 ] @
@miki208
Citat: Hehe,nije domaci,nego sam postavio ovu temu jer nigde na internetu ne mogu da pronadjem neke dobre zadatke iz programiranja pa sam odlucio da se ovde svi pomucimo malo xD.Hteo sam da zadaci krenu od onih laksih pa da svaki novi zadatak bude tezi.
evo zadatka za zagrevanje.
1.Napisi program koji ce ti prikazati prvih 15 elemenata Fibonicijevog niza: Fibonaccijev niz je niz brojeva sa osobinom da je svaki član niza osim prava dva jednak zbiru predhodna dva člana 1, 1, 2, 3, 5...
2.Napisi program kojim ces zameniti mesta elementima matrice:
a)preko glavne dijagonale
b)preko sporedne dijagonale
[ miki208 @ 01.12.2010. 20:23 ] @
Evo prvi zadatak moze ovako da se resi:
Code:
#include <iostream.h>
#include <cstdlib>
using namespace std;
int main(){
unsigned long next=0;
unsigned long last=1;
int i=0;
long zbir;
while(i<15)
{
i++;
cout<< last << endl;
zbir=next+last;
next=last;
last=zbir;
}
system("PAUSE");
return 0;
}
[ jzarko @ 01.12.2010. 22:10 ] @
@miki208
Evo ti jedan primer, takodje za vezan za fibinicijev niz.Ukucas redni broj elementa u nizu a program ti izbaci koji je to element.Problem je resen rekurzijom.
Ovaj primer je iz knjige Jesse Liberty.
Code:
#include <iostream>
using namespace std;
int fib(int n);
int main()
{
int n, answer;
cout << "Enter number to find: ";
cin >> n;
cout << "\n\n";
answer = fib(n);
cout << answer << " is the " << n << "th Fibonacci number\n";
return 0;
}
int fib (int n)
{
cout << "Processing fib(" << n << ")... ";
if (n < 3 )
{
cout << "Return 1!\n";
return (1);
}
else
{
cout << "Call fib(" << n-2 << ") and fib(" << n-1 << ").\n";
return( fib(n-2) + fib(n-1));
}
}
[ Nedeljko @ 02.12.2010. 08:58 ] @
Onaj rekurzivan algoritam računa Fibonačijeve brojeve u eksponencijalnom vremenu. Ovaj to radi u linearnom.
Code:
int fib(int n) {
if (n < 3) {
return 1;
}
int n2 = n >> 1;
int a = fib(n2);
int b = fib(n2 + 1);
if ((n & 1) == 0) {
return a*(2*b - a);
}
return a*a + b*b;
}
a može još brže - u vremenu 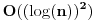 . [ itf @ 02.12.2010. 14:33 ] @
Hm.. kad smo već kod rekurzije.. Bio je jedan zadatak koji traži da program ispiše koliko puta se može pozvati rekurzivna funkcija void f(); prije nego što se dogodi stack overflow. Jasno, program se ne smije srušiti, već mora ispisati tu informaciju i normalno završiti s izvođenjem.
[ Nedeljko @ 02.12.2010. 15:55 ] @
Rešenje se može naći na stack overflow-u. Ime sajta lepo kaže šta se na njemu može naći. [ Nedeljko @ 03.12.2010. 10:34 ] @
Evo, kako bi mogao da izgleda efikasan algoritam za Fibonačija:
Code:
#include <iostream>
#include <cstdlib>
#include <map>
using namespace std;
class Fibonachi {
static map<int, long long int> cache;
public:
static long long int value(int n) {
if (n < 3) {
return 1;
}
map<int, long long int>::const_iterator i = cache.find(n);
if (i != cache.end()) {
return (*i).second;
}
int n2 = n >> 1;
long long int a = value(n2);
long long int b = value(n2 + 1);
long long int val = (n & 1) == 0 ? a*((b << 1) - a) : a*a + b*b;
cache.insert(pair<int, long long int>(n, val));
return val;
}
static void clear() {
cache.clear();
}
};
map<int, long long int> Fibonachi::cache;
int main() {
cout << "Zdravo" << endl;
for (int i = 1; i <= 10; ++i) {
Fibonachi::clear();
cout << Fibonachi::value(i) << endl;
}
system("pause");
return EXIT_SUCCESS;
}
Uzgred, kako da mi ES ofarba kod u skaldu sa C++ sintaksom? [ Nedeljko @ 04.12.2010. 19:00 ] @
Napisati program kome se unosi ispravna šahovska pozicija u kojoj je beli na potezu, od figura su na tabli samo kraljevi, beli konj i beli lovac i koji kao beli matira crnog kojim upravlja korisnik u ne više od 50 poteza.
[ Nedeljko @ 04.12.2010. 22:31 ] @
Samo da napomenem da za rešenje nije potrebno nikakvo poznavanje šahovske teorije osim pravila šahovske igre. Dakle, ne traži se implementacija postojećih algoritama za žive igrače. Zadatak se može rešiti i tako, ali se problem može rešiti programski daleko jednostavnije.
[ mihojla @ 06.12.2010. 17:12 ] @
Taj zadatak bi pre išao u forum matematika-topologija a ne c++
[ Nedeljko @ 06.12.2010. 22:13 ] @
Rešenje nema nikakve veze sa matematikom, pa ni sa njenom granom topologijom (sa kojom tek nema veze).
[ Nedeljko @ 06.12.2010. 22:19 ] @
Da si rekao da je za forum "Art of Programming", bilo bi na mestu, jer problem nema veze sa izborom programskog jezika. Sa matematikom ima veze onaj zadatak koji si ti postavio
Citat: mihojla: Program koji ce upisati brojeve od 1-125 u kocku 5x5x5 tako da zbir u svakoj koloni i svakom redu bude jednak. [ mihojla @ 07.12.2010. 10:43 ] @
Citat: Nedeljko: beli konj i beli lovac i koji kao beli matira Mislim da poslednji potez se igra lovcem tako da je potrebno saterati kralja u beli ćošak. Boga mi nije ni malo jednostavno u 50 poteza. [ Nedeljko @ 07.12.2010. 11:06 ] @
Ti razmišljaš o rešenju primenom šahovske teorije za koju sam napisao da nije potrebna. Postoji jednostavnije rešenje ako treba da ga izvršava računar, a ne čovek.
[ Nedeljko @ 07.12.2010. 14:27 ] @
Pa, evo, da dam ideju.
Poziciju cine raspored figura na tabli i informacija o tome ko je na potezu. Može se predstaviti sa 25 bitova. Dakle, ceo broj koji odgovara nekoj poziciji zvacemo njenim kodom. Naravno, neće svi brojevi u opsegu od 0 do 225-1 biti kodovi legalnih pozicija. Vrednošću pozicije smatracemo broj poteza potreban da crni bude matiran uz optimalnu igru oba igraca. Prvo treba izracunati niz v takav da je vi vrednost pozicije sa kodom i.
Najpre u petlji gde i ide od 0 do 225-1 ispitajmo da li je i kod legalne pozicije, pa ako jeste, onda u vi upišimo 0 ako je u njoj crni na potezu i matiran. 51 ako je pat pozicija (crni je na potezu i ne može da igra, a nije u šahu), kao i pozicije u kojima je crni na potezu i može odmah da pojede konja ili lovca, odnosno -1 u ostalim slucajevima. Ako i nije kod legalne pozicije, onda neka je vi jednako 51.
Zatim formirajmo petlju u kojoj k ide od 0 do 50 u kojoj radimo sledece:
U petlji gde i takode ide od 0 do 225-1 ispitajmo da li je vi=-1 i pritom je u odgovarajucoj poziciji beli na potezu, pa ako jeste, da li može odmah da pređe u poziciju sa kodom j tako da je vj=k. Ako može, onda izvršimo dodelu vrednosti k promenljivoj vi.
Potom u petlji gde i takode ide od 0 do 225-1 ispitajmo da li je vi=-1 i u odgovarajucoj poziciji je crni na potezu, pa ako jeste, da li bar jednim svojim legalnim potezom prelazi u poziciju sa kodom j tako da je vj=51. Ako je tako, onda dodelimo vrednost 51 promenljivojvi, a u suprotnom izvršimo dodelu vrednosti m promenljivoj vi, gde je m najveća od vrednosti vj takvih da crni mo\e odmah da pre]e u poziciju sa kodom j.
Na izlasku iz petlje sa brojačkom promenljivom k na sva mesta niza v čija je vrednost jednaka -1 upišimo 51.
Niz v je izračunat. Tačno značenje mu je sledeće: Ako je vi=51, onda je pozicija nelegalna ili crni može da se odbrani. Ako je beli na potezu u legalnoj poziciji sa kodom i, onda mu je uz najbolju odbranu crnog potrebno vi+1 poteza da ga matira. Ako je crni na potezu u legalnoj poziciji sa kodom i, onda crni može da se vadi vi poteza uz najbolju igru belog.
Napokon, evo najbolje strategije za oba igraca, nakon što je niz v izračunat.
Ako je beli na potezu u legalnoj poziciji sa kodom i, onda treba da igra potez koji ga prevodi u poziciju sa kodom j takvu da je vj=vi. Ako je crni na potezu u legalnoj poziciji sa kodom i, onda mu je najbolje da odigra potez koji ga prevodi u poziciju sa kodom j takvim da je vj=vi-1.
[ Nedeljko @ 07.12.2010. 14:32 ] @
Ima li nekoga zainteresovanog za implementaciju?
[ Nedeljko @ 17.12.2010. 15:30 ] @
Evo rešenja.
[ Nedeljko @ 17.12.2010. 16:30 ] @
Prilikom prvog pokretanja program izračunava potrebnu tabelu za šta mu je potrebno određeno vreme koje zavisi od brzine računara. Nakon nekog vremena od ispisa "Stage 33 white" se tabela snima na disk. Prilikom svakog sledećeg pokretanja tabela se učitava sa diska, pa nema čekanja na izračunavanje.
[ Sini82 @ 18.12.2010. 11:02 ] @
$ ./main
KnightAndBishop
Copyright (c) 2010 by Nedeljko Stefanovic, [email protected].
You are free to use, copy, modify and distribute it under the terms
of either version 2 or version 3 of the GNU General Public License
as published by the Free Software Foundation.
Data not present. Initialization
Stage 0 white
Svaka čast na zadatku i rješenju, program si stavio pod licencu.
U kom obliku se unose podaci? Možeš li navesti primjer unosa?
Da li je neko riješio ovaj problem (po meni ne bi trebalo da se ide dalje sa postavljanjem zadataka dok se on ne riješi):
Citat: mihojla:
Program koji ce upisati brojeve od 1-125 u kocku 5x5x5 tako da zbir u svakoj koloni i svakom redu bude jednak. ? [ Nedeljko @ 18.12.2010. 12:06 ] @
Evo primera ulaza
KnightAndBishop
Copyright (c) 2010 by Nedeljko Stefanovic, [email protected].
You are free to use, copy, modify and distribute it under the terms
of either version 2 or version 3 of the GNU General Public License
as published by the Free Software Foundation.
Data not present. Initialization
Stage 33 white
Saving data
Data saved
Enter the positions of the pieces
White king a8
White knight h2
White bishop e8
Black king c8
Turn (black or white) black
1. ... Kc7
2. Ka7 Kd8
3. Bc6 Kc7
4. Be4 K
Problem sa 5x5x5 kockom sam pokušavao da rešim i nisam uspeo, ali ako se zadaci ne budu postavljali i rešavali zbog toga, neće biti ništa od teme. [ atelago @ 19.12.2010. 10:41 ] @
Ja imam jedan zadatak za vas, ali ne znam da li da ga postavim. Smislio sam igru
(ne „igricu“) koja može da se postavlja u bezbroj varijanti i da se traži rešenje.
Nazvao sam je „Promenljivi lavirint“. Principijelno je vrlo jednostavna – ima svoje
mogućnosti i ograničenja tako da je naizgled jednostavna, ali stvarno ipak nije.
Mogu se postavljati određeni problemi ili mogu se postavljati krajnji ciljevi do kojih
treba da dođu dva suprotstavljena protivnika i t. d. i t. d.
Onaj što je izmislio šah trebalo je da kao nagradu dobije nekoliko godišnjih žetava
žita, a i ja bih hteo da dobijem bar neku kintu.
Kako?
Ako pokažem princip, stvar je za mene odmah propala što se tiče te kinte. Ima li
kakva mogućnost da nešto zaradim? Ne bi bilo nepošteno.
S druge strane i ovde se govori o nekom zajedničkom vlasništvu autora i ovog
foruma, ali ne znam kako to da protumačim. Postoji li u tom smislu neka zaštita?
Igru nije moguće napraviti od stvarnih elemenata poput šaha jer postoje određene
tehničke poteškoće, mada bi one mogle biti prevaziđene upotrebom elektromagneta
Najbolje i najlakše bi je bilo isprogramirati (a u tu drvenariju se uopšte ne razumem)
Naravno, radi se samo o programiranju mogućih poteza s obzirom na ograničenja
koja logički slede iz same fizičke konstrukcije.
Imate li neki savet?
[ Mihajlo Cvetanović @ 19.12.2010. 12:18 ] @
Moj savet ti je da istražiš na internetu da nije slučajno već izmišljeno to što si otkrio. Stvaranje promenljivih lavirinata ne postoji od juče. Slučajno baš naletih na knjigu u kojoj ima raznih glavolomki pa pretpostavljam i promenljivih lavirinata: http://www.amazon.com/Zen-Laby...azes-Connoisseur/dp/1402759878 . Na autorovom sajtu http://davephillipspuzzlemaze.com/ imaš jedan lavirint u kome miš treba da pojede sve sireve i izađe iz lavirinta, ali kako prolazi kroz lavirint kapije menjaju konfiguraciju lavirinta. [ Nedeljko @ 20.12.2010. 10:37 ] @
Citat: atelago: Onaj što je izmislio šah trebalo je da kao nagradu dobije nekoliko godišnjih žetava
žita
Mnogo više od nekoliko godišnjih žetava žita. Pitanje je da li je do dan-danas proizvedeno toliko žita u svetu. [ mihojla @ 16.02.2014. 13:11 ] @
Nisam baš vešt da taj program iskompajliram pod linuxom.
Primenom šahovske teorije može lako da se matira u najviše 30-ak poteza. U početku mi je delovalo komplikovano, ali posle nekoliko dana (nedelja) vežbe mogu da matiram sa najviše dva minuta za razmišljanje. Odnosno, mogao sam...
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|