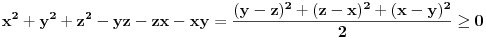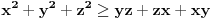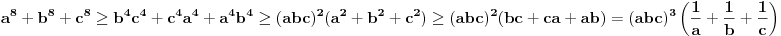[ Fermion @ 29.11.2010. 09:33 ] @
|
[ Nedeljko @ 29.11.2010. 10:42 ] @
To se svakako može dokazati primenom Mjurhedove teoreme.
[ Fermion @ 29.11.2010. 11:02 ] @
Da, ali je zadatak iz dela knige o nejednakostima gde se govori o odnosima između sredina, dakle trebalo bi da postoji neki elegantniji način da se pomoću toga dođe do rešenja.
[ Fermion @ 29.11.2010. 22:22 ] @
Hvala. Svaka čast na kratkom i efektnom dokazu.
U međuvremenu sam i ja uspeo na sličan način da dokažem ovu nejednakost, ali dužim putem. Pođimo od pretpostavke da je ispunjena nejednakost: 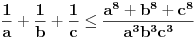 Pošto je a>0, b>0 i c>0, važi i 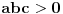 , kao i , kao i 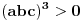 ako polaznu nejednakost pomnožimo sa ako polaznu nejednakost pomnožimo sa 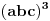 ne menja se znak kod nejednakosti pa važi: ne menja se znak kod nejednakosti pa važi: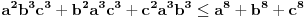 Ovo je ekvivalentno sa: 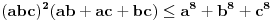 Dokažimo da je: 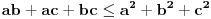 Nejednakost pomnožimo sa 2. 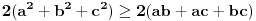 Odatle: 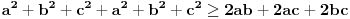 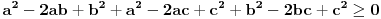 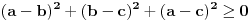 Zadnja nejednakost je jasno ispunjena, pošto je zbir kvadrata veći ili jednak 0. Ako se nejednakost 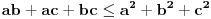 iskoristi u iskoristi u 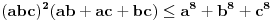 dobija se: dobija se: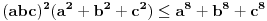 To je ekvivalentno sa: 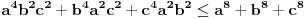 Treba dokazati da je: 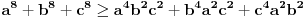 Slično kao i 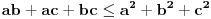 dokazuje se: dokazuje se: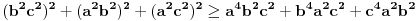 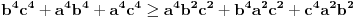 Preostaje da se dokaže da je: 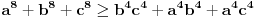 Kada se ovo pomnoži sa dva, dobijena nejednakost se transformiše u obilk: 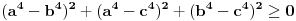 Ova nejednakost je zadovoljena za svako a, b, c>0, pa je polazna pretpostavka tačna, tj. važi: 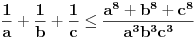 Jedakost važi ako i samo ako: 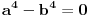 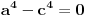 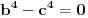 Prema tome jednakost se dobija ako i samo ako 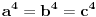 . .Pošto su a, b, c istoga znaka ovo je ekvivalentno sa 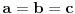 . .Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|