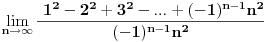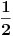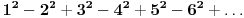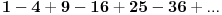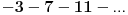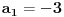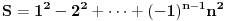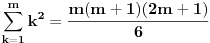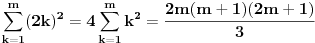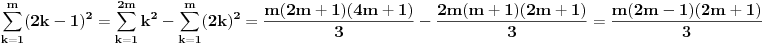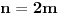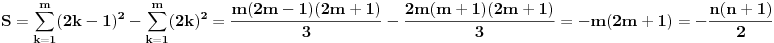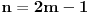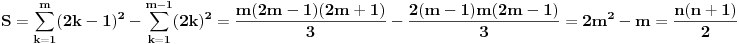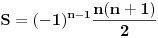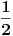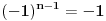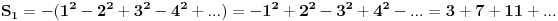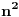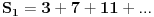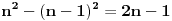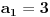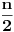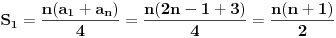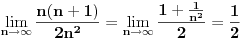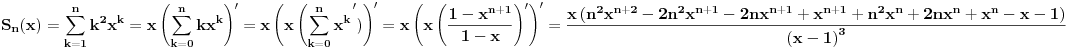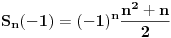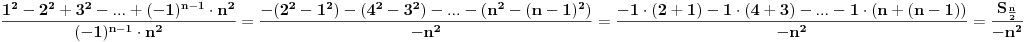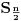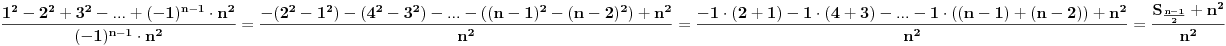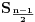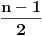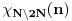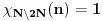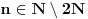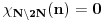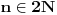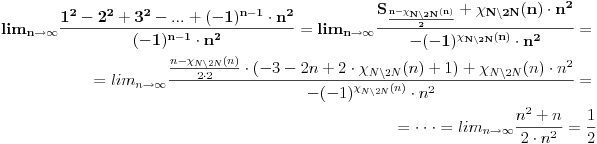[ Janinka @ 30.11.2010. 21:06 ] @
| Imam neke zadatke sa limesima i sve sam uradila osim jednog... Ide ovako lim (1^2-2^2+3^2-.....+(-1)^(n-1)*n^2)/((-1)^(n-1)*n^2)) , n->besk. Ideja mi je da razgledam brojilac kao razliku od sume kvadrata neparnih brojeva i sume kvadrata parnih brojeva, ali za prvu sumu znam formulu. to je (n(2n-1)(2n+1)/3) ako se ne varam, ali drugu sumu ne znam... Molila bih pomoc jer mi treba hitno... Znam da ne dajete resenja, ali stvarno mi je samo ovo ostalo i zapela sam... Unapred hvala! |