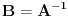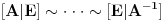[ R A V E N @ 02.12.2010. 16:38 ] @
|
[ Sini82 @ 02.12.2010. 17:28 ] @
Ako ti je lakše, izračunaj vrijednost njene determinante i svedi je na njoj inverznu matricu elementarnim transformacijama, zatim ih pomnoži. Dobićeš adjungovanu matricu.
[ R A V E N @ 02.12.2010. 18:39 ] @
Ustvari, ovi kofaktori mi i trebaju na prvom mjestu da bih našao inverznu matricu. Ako ima neki alternativni način za dobivanje inverzne matrice bez kofaktora, još bolje!
[ miki069 @ 02.12.2010. 18:55 ] @
Elementarne transformacije ne menjaju rang matrice:
1. Zamena mesta bilo kojim dvema vrstama (kolonama) 2. Množenje bilo koje vrste (kolone) brojem<>0. 3. Sabiranje bilo koje vrste (kolone) sa nekom drugom vrstom (kolonom). 4. Odstranjivanje (brisanje) vrste (kolone) čiji su svi elementi = 0. Kod Gaus-Jordanove metode za nalaženje inverzne matrice ne sme se koristiti transformacija broj 1. Transformacija broj 2 sme se koristiti samo ako ide istovremeno sa transormacijom broj 3. Transformacija broj 4 ne sme se koristiti i u tom slučaju matrica je singularna. [Ovu poruku je menjao miki069 dana 02.12.2010. u 20:42 GMT+1] [ Fermion @ 02.12.2010. 20:06 ] @
Citat: R A V E N: Ako ima neki alternativni način za dobivanje inverzne matrice bez kofaktora, još bolje! Ovde je lepo opisano kako se nalazi inverzna matrica. http://en.wikipedia.org/wiki/Invertible_matrix#Methods_of_matrix_inversion [ miki069 @ 02.12.2010. 21:50 ] @
Evo ti sa konkretnim priomerom: http://matematika.fkit.hr/novo...1/predavanja/Mat1_Lekcija6.pdf
Primer broj 8 je za inverznu matricu. Ostalo je za sisteme linearnih jednačina. [ Kolins Balaban @ 03.12.2010. 06:38 ] @
ja sam inverznu matricu uvijek rjesavao na ovaj nacin:
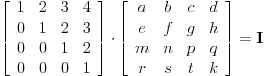 izmnozim s slijeve strane te dvije matrice, i izjednacim odgovarajuce "pozicije" sa lijeve i desne strane (ovdje mi je jedinicna matrica), i dobijem sistem linearnih jednacina koje se lako rjesavaju... na taj nacin nadjem brojeve a, b, c, d, e..... zapravo rukovodim se pravilom MATRICA*INVERZNA_MATRICA=JEDINICNA_MATRICA. Naravno, uslov det(MATRICA)<>0 i dalje mora biti zadovoljen! [ petarm @ 03.12.2010. 09:20 ] @
Citat: Kolins Balaban: ja sam inverznu matricu uvijek rjesavao na ovaj nacin: 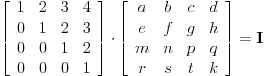 izmnozim s slijeve strane te dvije matrice, i izjednacim odgovarajuce "pozicije" sa lijeve i desne strane (ovdje mi je jedinicna matrica), i dobijem sistem linearnih jednacina koje se lako rjesavaju... na taj nacin nadjem brojeve a, b, c, d, e..... zapravo rukovodim se pravilom MATRICA*INVERZNA_MATRICA=JEDINICNA_MATRICA. Naravno, uslov det(MATRICA)<>0 i dalje mora biti zadovoljen! Mislim da ovaj nacin nije bas narocito brz! Usudio bih se reci da je ok samo za matrice reda 2. [ petarm @ 03.12.2010. 09:45 ] @
Citat: R A V E N: Data je matrica  i potrebno je da nađemo matricu njenih kofaktora (matricu njenih podeterminanti). Iako ova matrica ima poprilično nula, čime je posao olakšan i dalje je zadatak relativno delikatan. Postoji li neki lakši ili manje rizičniji način za pronalaženje matrice tih kofaktora? Možda nekom transformacijom matrice ili njene determinante? Kad sve sracunas inverzna matrica bi trebalo da izgleda kao 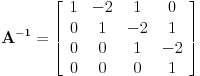 [ Kolins Balaban @ 03.12.2010. 09:49 ] @
znaci, imas 16 jednacina u ovom slucaju. jednacine su podjeljene u kao neke 4 grupe. ako rjesavas gauss-ovom metodom, postupak koji primjenis na jednu grupu sistema, je lako primljenjiv i na ostale 3 grupe jednacina:
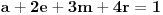 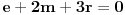 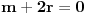 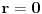 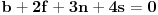 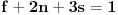 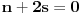 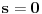 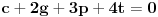 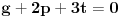 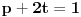 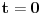 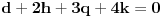 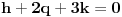 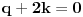 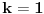 znaci, grupe su identicne, samo je desna strana jednacina drugacija.... rjesenje prve grupe: iz zadnje jednacine r uvaliti u predzadnju, slijedi m=0. m i r uvaliti u drugu, slijedi e=0, i na kraju sve poznato uvalis u prvu, slijedi a=1. potpuno isti metod primjenis na ostale tri grupe. naravno, ovo je jednostavna situacija, ali kad se uradi par inverznih na ovaj nacin, vjeruj mi teze je pogrijesiti nego kod onih kofaktora, tj. izracunavanja silnog broja determinanti 3x3.... [ petarm @ 03.12.2010. 10:12 ] @
Ok! Prihvatam da je opravdano koriscenje ovog postupka za 2x2 i retke matrice vecih dimenzija :) Svidja mi se sto kad krenes od cetvrte jednacine u svakoj od grupa prvi iz svake, drugi iz svake, treci iz svake i cetvrti iz svake ce ciniti po jednu vrstu inverzne matrice!
[ Kolins Balaban @ 03.12.2010. 10:38 ] @
da, rekao sam ovo je jednostavan primjer, i inv. sam nasao za 2 min. ali da su malo slozenije grupe jednacina, opet kad skontas koju s cim pomoziti, koju od koje dodati/oduzeti, onda to isto primjenis na ostale grupe.
[ Sini82 @ 03.12.2010. 11:10 ] @
[ R A V E N @ 03.12.2010. 13:26 ] @
Hvala svima na odgovorima, proučiću sve to.
Citat: miki069: Evo ti sa konkretnim priomerom: http://matematika.fkit.hr/novo/matematika 1/predavanja/Mat1_Lekcija6.pdf Primer broj 8 je za inverznu matricu. Ostalo je za sisteme linearnih jednačina. http://matematika.fkit.hr/novi_matematika1.html Dobre li stranice. Mnoge stvari su izložene i objašnjene. A kod nas, kod nas se sve prepisuje navrat-nanos sa prljavih tabli, i predavanja i zadaci. Uzalud im visoko poznavanje matematike kad su slabi u kvalitetnom prenošenju toga. Naučili su krive prakse predavanja koje se godinama prenose u radu. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|