[ Nikola 23 @ 03.12.2010. 23:07 ] @
Zna li neko kako se radi zadatak na slici, znam da je resenje -1/4, ali kako do toga doci na sto laksi nacin (cuo sam da moze na vise nacina), slabo se razumem u tu oblast, pa ako neko ume neka pokaze?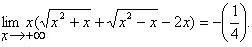 Hvala! |
|
[ Nikola 23 @ 03.12.2010. 23:07 ] @
[ Fermion @ 04.12.2010. 00:28 ] @
Izvinjavam se postavljaču teme što dodajem pitanje, ali vezano je za zadatak...
Krenuo sam da rešavam ovaj zadatak, težeći da ga rešim na što jednostavniji način i nisam dobio taj rezultat, ali siguran sam da imam grešku, jer pravo rešenje jeste -1/4. Ideja mi je bila da uvedem smenu 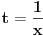 , sto znaci da je , sto znaci da je 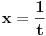 . .Traži se 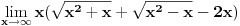 Pošto 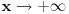 onda onda 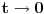 . .Onda se limes svodi na: 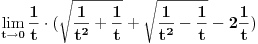 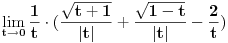 Zbog apsolutne vrednosti nalazimo levi i desni limes i oni su plus i minus beskonačno. To se naravno ne poklapa sa tačnim rešenjem. Gde sam pogrešio? [ atomant @ 04.12.2010. 01:04 ] @
[ Bojan Basic @ 04.12.2010. 02:04 ] @
Citat: Fermion: Zbog apsolutne vrednosti nalazimo levi i desni limes i oni su plus i minus beskonačno. Nisam siguran da te razumem. U zagradi imaš izraz oblika  , kako si mislio da se s tim izboriš? Ujedno, apsolutna vrednost je nepotrebna, jer , kako si mislio da se s tim izboriš? Ujedno, apsolutna vrednost je nepotrebna, jer 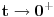 . Tvoja ideja može se nastaviti svođenjem svega na jedan razlomak i dvostrukom primenom L’Opitalovog pravila. . Tvoja ideja može se nastaviti svođenjem svega na jedan razlomak i dvostrukom primenom L’Opitalovog pravila.[ Nedeljko @ 04.12.2010. 09:44 ] @
[ Fermion @ 04.12.2010. 12:30 ] @
Citat: Bojan Basic: Nisam siguran da te razumem. U zagradi imaš izraz oblika  , kako si mislio da se s tim izboriš? Ujedno, apsolutna vrednost je nepotrebna, jer , kako si mislio da se s tim izboriš? Ujedno, apsolutna vrednost je nepotrebna, jer 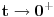 . Tvoja ideja može se nastaviti svođenjem svega na jedan razlomak i dvostrukom primenom L’Opitalovog pravila. . Tvoja ideja može se nastaviti svođenjem svega na jedan razlomak i dvostrukom primenom L’Opitalovog pravila.Tako sam to i zamislio, samo sam tražio i 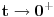 i i 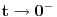 , s tim što je za zadatak bitna samo prva od njih, nisam to naglasio. Međutim ja sam pogrešio u sređivanju koje nisam napisao u poruci i zato sam našao te vrednosti limesa koje ne odgovaraju stvarnoj. , s tim što je za zadatak bitna samo prva od njih, nisam to naglasio. Međutim ja sam pogrešio u sređivanju koje nisam napisao u poruci i zato sam našao te vrednosti limesa koje ne odgovaraju stvarnoj.Zaista, ako se postupak nastavi: 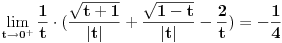 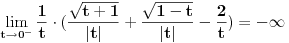 Naravno, za zadatak je bitna vrednost: 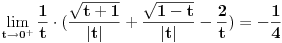 To je ujedno i tražena vrednost limesa. [ Fermion @ 04.12.2010. 14:11 ] @
[ Sini82 @ 04.12.2010. 15:03 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|