Pretpostavimo suprotno.

Dakle postoji konačan broj prostih brojeva . Svi ostali prirodni brojevi posle različiti od 1 tada trebaju biti složeni.

Tada je i broj složen.

Da bi bio složen, on mora biti deljiv nekim od onih prostih brojeva, a jasno da se takvim deljenjem dobija ostatak jedan.

Kontradikciija.

Prema tome postoji beskonačno mnogo prostih brojeva.

Inače ovaj dokaz je smislio Eukllid.

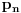
Na ovaj način se može naći i gornja granica za , -ti prost broj.

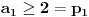
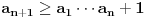
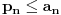
Neka je bilo koji niz takav da važi i . Tada je za svaki prirodan broj .

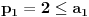
Zaista, . Uz odgovarajuću induktivnu hipotezu je .

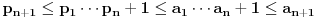
Nije teško proveriti da ovaj uslov ispunjava niz .

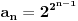
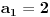
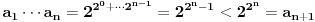
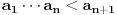
Zaista, i , pa iz sledi da je .

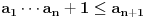
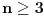
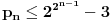
Sada nije teško dokazati da za važi . Naravno, postoje i mnogo bolje procene.