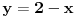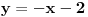Pošto se odrede sve moguće +/- kombinacije sa apsolutnim vrednostima dobija se nekoliko (ovde konkretno 4) linearnih funkcija. Grafik linearne funkcije lako se crta. Ta četiri grafika će ovde graditi kvadrat čiju površinu treba izračunati.

Dobijene linearne funkcije su:y=4-x;y=2-x;y=6+x i x=y
aha ali kako da izracunam povrsinu ono moze preko jedinicnih
duzi ali moze li na neki grugi nacin i kako

Tri jednačine su dobre, ova nije:

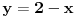
Treba da bude:


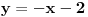
Treba da preciziraš na kom intrevalu važi koja relacija.
Recimo pomenuta je za x<-1 i y<2.

Pošto to učiniš nacrtaj grafike tih funkcija. Dobićeš kvadrat.

Temena tog kvadrata su presečne tačke odgovarajućih grafika. Dakle uzimaju se jednačine pravih i rešavaju kao sistem. Ta zajednička rešenja su ujedno i koordinate temena tražene figure. Takav postupak treba primeniti na sva četiri temena i tako se dobijaju koordinate.

Pitagorinom teoremom nalaze se dužine stranica figure, i u ovde su sve četiri jednake jer je u pitanju kvadrat. Dalje se lako nalazi površina kvadrata.

Može i pomoću analitičke geometrije. Treba primetiti da iz koeficijenta pravca dobijenih jednačina prave sledi da postoje dva para paralelnih prava i da su uglovi između svake dve koji se seku 90 stepeni. Odatle sledi da je u pitanju ili pravougaonik ili kvadrat. Zatim nalazimo koordinate dva temena kao presečne tačke odgovarajućih jednačina prave koje odgovaraju stranicama. Onda se računa rastojanje između svake dve. Pošto je rastojanje odgovarajućih tačaka jednako zaklučujemo da je u pitanju kvadrat. Odatle se lako računa površina.

Još jednostavnije, površina se može izračunati i tako što se dobijeni kvadrat podeli na pravougle trouglove, a zatim se površina cele figure dobije kao zbir površina trouglova od kojih se ona sastoji.

Kada povuces pravu y=2, imas 2 trougla (1 i 2), istih povrsina. Sada samo izracunas povrsinu unutar pravih. P=18

Moze ovo naravno i preko integrala, ali ovako je cini mi se lakse za razumevanje.

Da, lepa ilustracija.

Dobija se 18 i na način koji sam pomenuo.

Inače prava figura je kvadrat, kao što sam gore obrazložio, ovde na slici je to u obliku romba samo zbog razmera po osama.