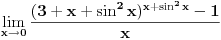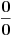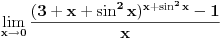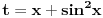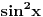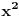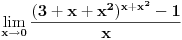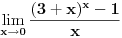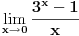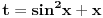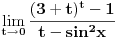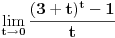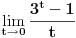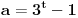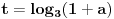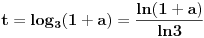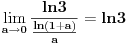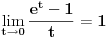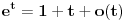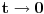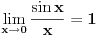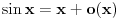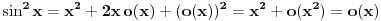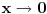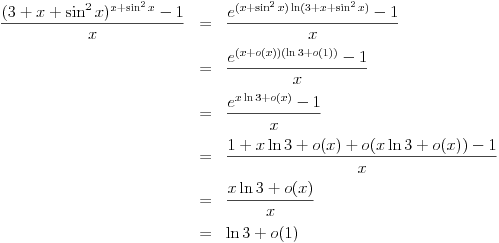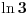[ ___ @ 06.12.2010. 23:46 ] @
|
| Ne stojim baš najbolje, tako reći nikako, s latexom, pa sam "nacrtala" zadatak.
Trebalo bi da se radi o računu s malim o, ali nikako ne mogu da se iskobeljam.
Pa, ako neko ima vremena i umeća...hvala unapred :)
http://img213.imageshack.us/i/72852129.png/ |
[ Nedeljko @ 06.12.2010. 23:57 ] @
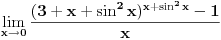 .
Dobro, kako si krenula? [ Fermion @ 07.12.2010. 06:59 ] @
Pošto je ovde neodređenost oblika 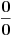 može se primeniti Lopitalovo pravilo.
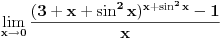
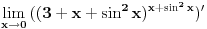
[ ___ @ 07.12.2010. 07:06 ] @
Nedeljko, hvala, ali ne smem da koristim izvod, zato sam i naglasila da je u pitanju račun s malim o :)
[ Nedeljko @ 07.12.2010. 08:26 ] @
Pa, dobro, reci kako si krenula, pa ćemo da kompletiramo.
@Fermion
Lopitalovo pravilo nije uvek dozvoljeno na ispitu.
[ Fermion @ 07.12.2010. 08:35 ] @
Citat: Nedeljko:
Lopitalovo pravilo nije uvek dozvoljeno na ispitu.
Znam, previše olakšava rešavanje nekih "težih" limesa.
Citat: ___: Nedeljko, hvala, ali ne smem da koristim izvod, zato sam i naglasila da je u pitanju račun s malim o :)
Nemam vremena sad da rešavam zadatak, ali čini mi se da bi smena 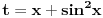 mogla biti pogodan pristup. [ Nedeljko @ 07.12.2010. 09:25 ] @
Citat: Fermion: Znam, previše olakšava rešavanje nekih "težih" limesa.
Nije to uvek razlog. Ponekad se zaista zabrani upotreba radi provere poznavanja drugih metoda, ali najčešće to nije razlog. Studenti bi primenjivali Lopitalovo nekritički, bez obzira da li ga je praktično primeniti ili ne (recimo da je izvod vrlo složen, a da Lopitalovo pravilo treba primeniti više puta). Stoga mislim da se Lopitalovo pravilo načelno zabranjuje da bi studenti manje padali na ispitu. Naravno, ako neko tačno reši zadatak primenom Lopitalovog pravila, naravno da će se zadatak priznati u celini, osim ako nije izričito zabranjeno u zadatku, čija je suština provera poznavanja drugih metoda. Hoću da kažem da se implicitna zabrana obično ne primenjuje. [ different @ 07.12.2010. 22:43 ] @
Evo mala pomoc,
prvi sabirak brojnika napisi kao exp(ln (prvi sabirak)) a onda izvrsi aproksimaciju, (e^u-1)/u je ekvivalentno sa "1" kad je "u" dovoljno malo...dalje probaj sam pa cemo nastaviti...
[Ovu poruku je menjao different dana 08.12.2010. u 19:26 GMT+1]
[Ovu poruku je menjao different dana 09.12.2010. u 07:48 GMT+1]
[ miki069 @ 09.12.2010. 06:47 ] @
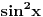 za x bliske 0 je blizak sa 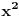 ,
Tako da je limes "blizak" sa:
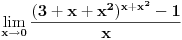
Za x bliske 0 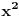 je "zanamarljiv" u odnocu na x,
pa je limes "blizak" sa:
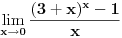
Što je dalje "blisko" sa:
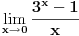
Rezultat je ln(3) što je približno 1.098612289
Samo je prva aproksimacija potkovana tabličnim limesom.
Ove ostale su na osećaj.
Excel kaže da je rezultat ln(3) tačan.
[Ovu poruku je menjao miki069 dana 09.12.2010. u 08:05 GMT+1][ Fermion @ 09.12.2010. 07:25 ] @
Slično bi se dobilo i smenom 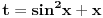 koju sam pomenuo:
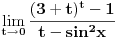
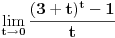
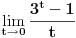
Sada uvedemo smenu: 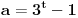 , 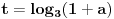
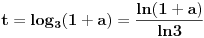
Kada se to vrati u polzan limes:
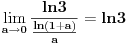
Isto bi se moglo dobiti i razvojem u red oko nule, tj. ln3 bi bio jedini član razvoja koji nije pomnožen sa x koje je blisko nuli, pa stoga je ln3 traženi limes.
[Ovu poruku je menjao Fermion dana 09.12.2010. u 09:16 GMT+1][ Fermion @ 09.12.2010. 08:37 ] @
Pomoću Lopitalovog pravila se inače isto dobije ln3.
Ovo je dobar primer toga da ovo pravilo nije uvek lakši put do rešenja nekog limesa.
[ Nedeljko @ 09.12.2010. 09:03 ] @
Hajde da napišem strogo rešenje sa malim "o".
Iz 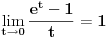 sledi da je 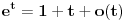 kad 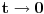 .
Iz 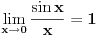 sledi da je 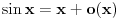 , a samim tim i 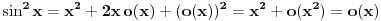 kad 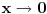 .
Dakle,
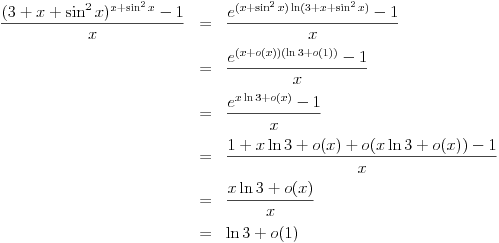
kad 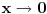 , pa je traženi limes jednak 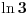 [Ovu poruku je menjao Nedeljko dana 09.12.2010. u 13:31 GMT+1]
[Ovu poruku je menjao Nedeljko dana 09.12.2010. u 13:31 GMT+1][ Sini82 @ 09.12.2010. 11:45 ] @
Ima štamparska greška na dva mjesta, ostalo je sve u redu (na jednom mjestu pise 2 umjesto 1,na drugom u brojiocu imamo viška -1).
[ Nedeljko @ 09.12.2010. 12:31 ] @
Dvojku sam ispravio, ali ne nalazim gde to ima -1 viška.
[ Sini82 @ 09.12.2010. 12:35 ] @
U pravu si, nisam dobro gledao. Moja greška, svaka čast na rješenju.
[ ___ @ 09.12.2010. 14:17 ] @
Stvarno, svaka čast, i puno hvala :)
[ Nedeljko @ 09.12.2010. 15:34 ] @
Citat: miki069: Excel kaže da je rezultat ln(3) tačan.
Šta ti ovo znači? Koliko ja znam, eksel nema funkciju računanja limesa. [ blackholemix @ 09.12.2010. 23:44 ] @
Lopitalovo pravilo je jedno od "najglupljih", totalno mašinski većina učenika, studenata to primenjuje, i mnogi pogreše u računu, ili npr. zaborave kada ono sme da se koristi primenjujući ga n-ti put, ili se desi da ne srede dobro izraz koji imaju i deluje im da je neodređen, a on bude određen limes i onda primene Lopitalovo i dobiju nešto levo.
Najpraktičnije je korišćenje Tejlora, tj. Maklorena i tu se vidi da li neko oseća šta je granična vrednost, šta brže teži čemu i sl. Naravno ne može uvek ni Makloren, ali nekad se može smenama namestiti na njega.
Moj savet, zaobiđite Lopitala. :)
[ miki069 @ 09.12.2010. 23:45 ] @
Nema Excel limese.
Odradio sam funkciju koja je bila pod limesom u zavisnu od x.
Umesto x stavio 0.00000000000001 i dobio, radi provere, navedeni rezultat ln(3)
na koji sam "tipovao" od početka.
Svaka čast na rešenju.
[Ovu poruku je menjao miki069 dana 10.12.2010. u 00:57 GMT+1]
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|