Odrediti cele brojeve a i b....

[ edisnp @ 07.12.2010. 19:49 ] @

Odrediti cele brojeve a i b tako da 1+koren iz 3, bude
resenje jednacine ax^2+bx+12=0.

[ atomant @ 07.12.2010. 20:09 ] @

Pa ubaci u

vrednost x (

) i dobices jednu jednacinu.
Drugu jednacinu ces dobiti kada u

ubacis

.
Imaces sistem 2x2, a to sigurno umes i sam da resis :)

I da, ne dobiju se celi brojevi.

[ edisnp @ 07.12.2010. 20:20 ] @

Ovo mi nije jasno kako ste dobili dP(x)/dx=2ax+b

[ Nedeljko @ 07.12.2010. 20:29 ] @

Obzirom da je broj

iracionalan, a brojevi

celi, mora biti

, a samim tim i

.

Dakle,

[ lonelyrider_44 @ 07.12.2010. 20:31 ] @

Ja sam ishao drugim putem.

pa je

Kao i u prethodno ponudjenom reshenju, dobije se sistem jednachina. Reshavanjem sistema, dobije se da je a = -6 , b = 12

Izvinjavam se na izgledu latex-a, ne vidim gde greshim u sintaksi, a on prikazuje kako prikazuje.

[ edisnp @ 07.12.2010. 20:40 ] @

Hvala svima ovo je vise nego dovoljno!!!!!

[ Fermion @ 07.12.2010. 20:45 ] @

Pošto je koren jednačine

i broj

je koren ove jednačine.

Tražena jednačina je:

Mnženjem sa -6 dobija se:

Odatle se nalazi a=-6, b=12

[ Fermion @ 07.12.2010. 21:25 ] @

Citat:

lonelyrider_44:
Izvinjavam se na izgledu latex-a, ne vidim gde greshim u sintaksi, a on prikazuje kako prikazuje.

Formulu treba da pišeš u istom redu kao i TEX oznake. Evo kako izgledaju te iste formule, bez popravki, osim pomenutog spajanja.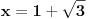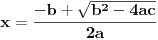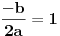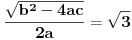

[ lonelyrider_44 @ 07.12.2010. 21:58 ] @

Hvala na ispravci, primljeno k'znanju za ubuduce.

[ Nedeljko @ 08.12.2010. 09:16 ] @

@Fermion

Fali ti dokaz da nema drugih rešenja.

[ Fermion @ 08.12.2010. 09:35 ] @

Citat:

Nedeljko: @Fermion

Fali ti dokaz da nema drugih rešenja.

Pošto je:

Pošto je rešenje

, onda je ovo racionalno

(jer znamo da su brojevi a i b celi), a iracionalni koren

Sad da ne bih rešavao sistem, primetim da je drugo rešenje slično, samo ima minus ispred korena. Tako sam zaključio da ako je rešenje jednačine

, onda je i

[ Nedeljko @ 08.12.2010. 11:21 ] @

Tako već može. U prethodnoj poruci si napakovao jednačinu i pomnožio je sa -6. Sada je OK.

[ Fermion @ 08.12.2010. 19:20 ] @

Tamo sam prosto napisao da ako je koren jednačine taj da onda mora biti baš onakav drugi, nisam naveo dokaz tog tvrđenja jer sam smatrao da je to sasvim jasno. Naravno trebao sam precizirati kako sam došao do tog zaključaka.

[ blackholemix @ 08.12.2010. 20:42 ] @

U matematici svako tačno rešenje je OK, ali postoje ona koja zovu elegantnija :) To je upravo Nedeljkovo, jer on ide prirodnim putem i to da su a i b celi brojevi upotrebi baš kada treba. Fermion, prvo tvrđenje si napisao tako da neki mogu da pomisle da to uvek važi, a ne važi uvek.

[ Fermion @ 08.12.2010. 21:35 ] @

Citat:

blackholemix: U matematici svako tačno rešenje je OK, ali postoje ona koja zovu elegantnija :) To je upravo Nedeljkovo, jer on ide prirodnim putem i to da su a i b celi brojevi upotrebi baš kada treba. Fermion, prvo tvrđenje si napisao tako da neki mogu da pomisle da to uvek važi, a ne važi uvek.

Naravno, samo sam ponudio još jedan način na koji se zadatak može rešiti.

Ono tvrđenje važi pod uslovom da su a i b celi brojevi.

_{[Ovu poruku je menjao Fermion dana 08.12.2010. u 22:52 GMT+1]}