Teorema: Ako su

i
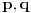
celi brojevi takvi da je
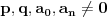
,
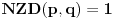
i

za
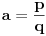
, onda
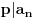
i
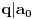
.
Dokaz: 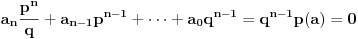
, odakle
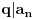
i
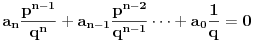
odakle
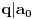
.
Posledica: Ako je

racionalan broj koji je koren polinoma sa celim koeficijentima i vodećim koeficijentom jednakim jedinici, onda je

ceo broj.
Napomena: Ova teorema se često koristi da bi se odredio konačan skup S racionalnih brojeva van koga sigurno nema racionalnih korena polinoma sa racionalnim koeficijentima, da bi se onda isprobavanjem elemenata skupa S pronašle sve racionalne nule polinoma.