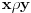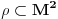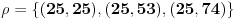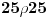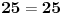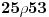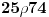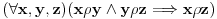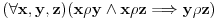Ovo je binarna relacija koju ćemo primeniti na skup M.

Pri tom su x i y u stvari vrednosti koje se biraju iz tog skupa.

Relacija ro određuje da prva cifra broja x manja od druge cifre broja y.

Nisam siguran šta podrazumeva tabela, ali pretpostavljam da je u pitanju ovo:




Što se tiče svojstava:
1)Refleksivnost

Nije refleksivna, tj. nisu svi elementi u relaciji sa samim sobom.

2)Ako je x u relaciji sa y onda nije i y u relaciji sa x, što mora da važi za svako x, y, prema tome nije ni simetrična.

3)Nije asimetrična jer ako je x u relaciji sa y i y u relaciji sa x iz toga ne sledi da je x=y za svako x,y

Napominjem da sam jako malo radio sa relacijama i moguće da sam stoga dopustio grešku (ili čak i više njih).

_{[Ovu poruku je menjao Fermion dana 08.12.2010. u 23:55 GMT+1]}

M={25,53,71,74}. akko prva cifra od x je manja od druge cifre od y; .

jer vrijede nejednakosti: 2<5, 2<3 i 2<4. Ispitajmo osobine relacije :

(R) Nije refleksivna (53 nije u relaciji sa 53).
(S) Nije simetrična (25 je u relaciji sa 53, obratno ne važi).
(AS) Jeste antisimetrična ( i ).
(T) Jeste tranzitivna ( i ; i ).

Dopustio sam jednu grešku u tabeli:




I da pogrešio sam i u vezi asimetrjie, jer ako važi da je i x u relaciji sa y i y u relaciji sa x tada su x i y zaista jednaki, u ovom slučaju x i y imaju vrednost 25.

Nije tranzitivna... Iz 25 u relaciji sa 53 i 25 u relaciji sa 74 ne sledi da je 53 u relaciji sa 74.

Griješiš.

Tranzitivnost:

Nisam bio siguran da li je tranzitivnost:

ili:


Nego, ja sam baš danas našaso ovaj zadatak u "Tangenti" br. 61 i piše u rešenju da je relacija samo antisimetrična, pa sam pretpostavio da je ovo drugo, mada je to tamo bez obrazloženja.

S obzirom da je ovo prvo, rekao bih da relacija jeste tranzitivna.

Znaju i oni pogriješiti, dobro je da razmišljaš svojom glavom.

Znamo da je relacija <= relacija poretka (RAST). Kada bi definicija tranzitivnosti bila drugacija, dobili bi da vrijedi jednakost bilo koja dva realna broja.

Npr. iz 2<=3 i 2<=5 dobili bi 3<=5, isto tako iz 2<=5 i 2<=3 dobili bi 5<=3; dakle, 3=5.

Da, ako se ima u vidu da je relacija poretka obavezno tranzitivna relacija jasno da ona moja druga definicija nema smisla... Vrlo ilustrarivan primer.

Tvoja druga definicija tranzitivnosti ima smisla samo za simetrične relacije što u navedenom primjeru nije slučaj.