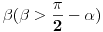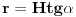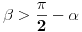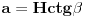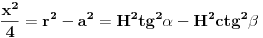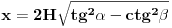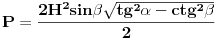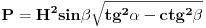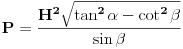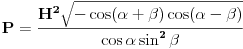Pokušao sam da uradim zadatak i za slučaj da kupa nije prava.

Neka je l projekcija visine presečnog trougla na pravac prečnika baze koji je normalan na tetivu koja pripada tom trouglu (osnovicu).

Tada je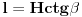

Rastojanje između presečne tačke kružnice prave koja leži na pomenutom prečniku i normale iz vrha na taj pravac je: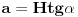


Rastojanje centra baze od tacke preseka visine i visine presecnog trougla koja sece pomenutu tetivu je: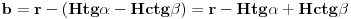


Povrsina presecnog trougla je: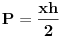


Pri tom je h: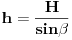


Stranicu x nalazimo iz: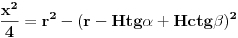


Treba još r izraziti preko H i poznatih uglova.

Iz kosinusne teoreme: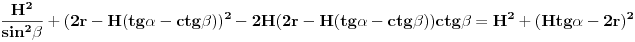


Odatle se nalazi r, zatim x i tražena površina.

Koje od ova dva rešenja je tačno?



_{[Ovu poruku je menjao Fermion dana 12.12.2010. u 11:53 GMT+1]}

Treba .

Takođe, umesto



piši

Hvala.

Ova konačna formula mi je štamparskom greškom ispala takvom...

Rešenje iz časopisa je:


Pošto ova formula baš i ne liči na ono rešenje, pretpostavio sam da sam pogrešio. Tek sam sad ispitao i dokazao ekvivalentnost rešenja.

A da li mi je ono drugo rešenje tačno za slučaj da kupa nije prava?

Ovaj deo ne razumem.

Dužina projekcije izvodnice na pravac prečnika koji je normalan na tetivu kruga (osnove kupe) koja je stranica trougla u preseku.

Odnosno ta duž, izvodnica i visina obrazuju pravougli trougao. Ta duž se u njemu nalazi naspram ugla .

Šta predstavlja ugao u slučaju kose kupe?

U slučaju kose kupe zadatak ne bi bio postavljen kako treba. Radi se o pravoj kupi.

U mom rešenju to je ugao između jedne izvodnice kupe i i normale na ravan osnove iz vrha kupe.



Shvatam, samo sam pitao da budem siguran.

Hvala svima.

Jel moze neko da mi napravi razliku izmedju paralelepipeda i parelelopipeda (ako postoji, a verujem da postoji)? Hvala! :D

Nema razlike.

Ali u zbirci koju ja koristim ( Vene 3), u odeljku za obrasce stoji ovako: Povrsina paralelepipeda je P=2(ab+ac+bc), V=abc .... Sto znaci da misle na kvadar. A posle u zadacima pominju paralelopiped ( osnova i bocne strane su paralelogrami ), ili prav paralelopiped ( osnove su dva paralelograma, a bocne strane 4 pravougaonika ). Jedino ako su ispustili da kazu da je taj paralelepiped pravougli, tj bio bi kvadar.

Pusti Venea. Uzmi neku drugu zbirku. Preporučujem ti krugove zbirke za srednju školu.

Prema nastavnom planu, kod nas, u upotrebi je VENE. I moramo da se bakcemo sa beskonacno mnogo gresaka, i ne samo u resenjima, vec i u tekstovima zadataka. Svake godine stampaju nova izdanja, ali, naravno, greske ne ispravljaju. A ovo me je bas zacudilo, jer se na vise mesta termin paralelepiped upotrebljava u znacenju kvadra.

Batali plan. Ako si profesor, radi po krugovim zbirkama, a ako si đak, opet po krugovim i super ćeš proći na pismenom. Nije stvar u tome da naštrebaš ne znam koliko Veneovih pogrešnih zadataka, već da naučiš gradivo i onda nećeš imati problema na pismenom.

Koja je razlika između Krugovih i Veneovih zbirki? Može li neko da ih uporedi? Zašto su Krugove bolje od Veneovih, može li neko da obrazloži? Hvala.

Moja profesorica je ove godine zahtevala od nas da svi kupimo Krugovu zbirku za drugi razred.Prosle godine jesmo koristili Venea i Matematiskop(ponekad).Meni se licno mnogo vise svidja Krugova zbirka nego Veneova,zato sto na prvi pogled nema gresaka i u krogovim zbirkama svaka obast je podijeljena na lakse(osrednje zadatke) teze i najteze,jednostavno bolje je u krugovim zbirkama vrsen odabir zadatak od laksih ka tezim ,sto je donekle i logicno jer je jedan od autora i direktor matematicke gimnazije,dok se u ostalim zbirkama u tome nije vodilo racuna, recimo u matematiskopu za drugi razred toga nema,sve je izmijesano,mozes da radis neki zadatak recimo,a da nemas pojma da je recimo bio na nekom drzavnom takmicenju il; okruznom..

U Veneovoj zbirki zadaci su poređani od lakših ka težim, samo što to nije obojeno kao u Krugovoj. Mislim da je Veneova zbirka sasvim solidna. Nađe se i nekoliko težih takmičarskih zadataka. Na kraju zbirke postoje posebno odvojeni RAZNI ZADACI sa raznih takmičenja. A, što se grešaka tiče, pa nađe se tu po neka... Nije strašno!

Na kraju Veneove zbirke postoji taj odeljak sa tezim zadacima,u tom odeljku se nalaze zadaci iz svih oblasti pomijesani,a u Krugovoj zbirci iza svake oblasti posebno se nalazi taj odeljak sa mnogo vise tezih zadataka .A u toj rubrici RAZNI ZADACI slabo se nadje neki da je sa takmicenje obicno je to sa nekih prijemnih.

"...beskonacno mnogo gresaka, i ne samo u resenjima, vec i u tekstovima zadataka..."

Ja ima Vene 3 i Vene 4. Izdanja iz 1980 i neke.
Rešenja i ne gledam.
U tekstovima zadataka ne mogu da pronađem konačno, a kamo li beskonačno grešaka.
Za ovih 30-godina, valjda su smanjivali broj grešaka, a ne povećavali.
Gde nalazite greške u tekstovima zadataka?
Rešenja ne komentarišem. Sigurno je da ih ima.