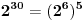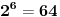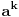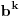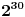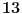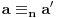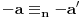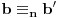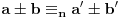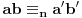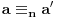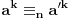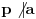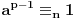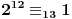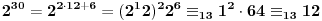[ edisnp @ 14.12.2010. 22:12 ] @
|
| Da li bi neko mogao da mo malo pojasni"Kongruencije po modulu"
ili sta to znaci dosao sam do par zadataka koje nikako ne uspevam da resim
nije mi jasna na primer sledeca definicija:
Za dva cela broja a i b kaˇzemo da su kongruentna po modulu n ukoliko n | a − b i zapisujemo
a ≡ b (mod n) ili a ≡n b.Neznam kako da to primenim dobro bi mi dosal bilo kakva pomoc.HVALA! |
[ Fermion @ 14.12.2010. 22:22 ] @
Pokušaću da na intuitivnom nivou predstavim značenje kongruencija. Kada kažeš da je a kongruentno b po modulu n to u stvari znači da pri deljenju a sa n dobijaš ostatak b.
Evo par primera.
5 je kongruentno 1 po modulu 4.
111 je kongruentno 11 po modulu 100.
123 je kongruentno 3 po modulu 120.
S tim što recimo može da bude i ovako:
9 kongruentno -1 po modulu 5.
Sasvim logično, kongruencije se koriste kod dokazivanja deljivosti i traženja ostataka pri deljenju.
[ edisnp @ 14.12.2010. 22:43 ] @
Odrediti ostatak pri deljenju 2^30 sa 13.
To zapisujemo ovako 2^30kongruentno n (mod 13)
i dalje neumem da nastavim zbunjuje me ovaj eksponent 30.
[ Fermion @ 14.12.2010. 23:01 ] @
Treba primetiti da je
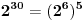
. Pošto je
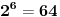
, a 64 je kongruentno -1 po modulu 13 (65=5*13) obe strane možemo stepenovati sa 5, pa je polazni broj kongruentan sa -1 po modulu od 13.
[ Fermion @ 14.12.2010. 23:07 ] @
Dakle eksponent ne predstavlja problem, kongruencije se uglavnom i koriste u zadacima takvog tipa. Treba samo znati pravilo da ako je a kongruentno b po modulu n, tada je i
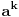
kongruentno
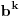
po modulu n.
[ Nedeljko @ 15.12.2010. 08:29 ] @
Odrediti ostatak od
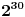
po modulu
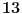
.
OK, prvo treba znati da važe sledeći zakoni:
1. Ako je
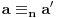
, onda je
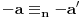
.
2. Ako je
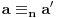
i
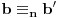
, onda je
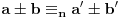
i
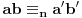
.
3. Ako je
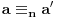
, onda je
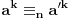
.
4. Za ma koji prost broj

i ceo broj

takav da
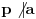
je
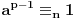
.
Dakle,
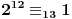
, pa je
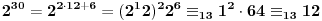
.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.