Dakle, od prve jednačine oduzmi treću, od druge prvu, a treću jednačinu zadrži.
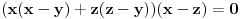
,
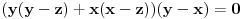
,
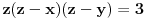
.
Prvu jednačinu podeli sa

, a drugu sa
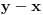
. Ovde se koristi uslov
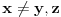
.
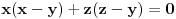
,
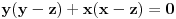
,
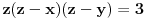
.
Od druge jednačine oduzmi prvu.
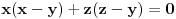
,
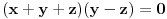
,
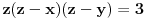
.
Podeli drugu jednačinu sa
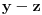
Kada se
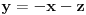
zameni u prvoj jednačini, a potom prva jednačina podeli sa
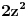
dobija se sistem
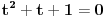
,
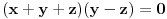
,
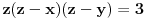
,
gde je
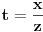
. Ovde smo iskoristili uslov
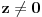
. Dakle,

je jedan od dva primitivna treća korena iz jedinice. Zbog simetrije isto važi i za
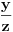
. Zbog
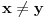
, brojevi

i
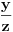
su različiti primitivni treći koreni iz jednice. Znači,
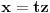
,
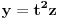
,
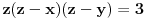
.
Zamenjujući

i

u trećoj jednačini i uzimajući u obzir da je
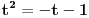
i
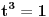
i potom deleći treću jednačinu sa

dobija se da je
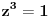
.
Dakle,
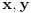
i

su međusobno različiti treći koreni iz jedinice.