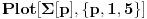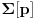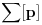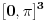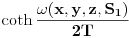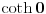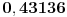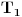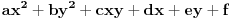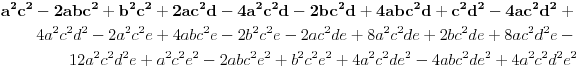[ petarm @ 17.12.2010. 16:09 ] @
|
[ atomant @ 17.12.2010. 17:23 ] @
Mislim da ce ti javiti gresku, jer ova suma nema smisla bez granica.
[ petarm @ 17.12.2010. 17:46 ] @
[ atomant @ 17.12.2010. 18:33 ] @
[ petarm @ 18.12.2010. 15:20 ] @
Mrzim Mathematicu! :( Moze li neko da mi objasni zasto ovde u poslednjem koraku ne dobijam brojnu vrednost i sta treba da uradim ne bih li je dobio?
[Ovu poruku je menjao petarm dana 18.12.2010. u 16:40 GMT+1] [ Bojan Basic @ 19.12.2010. 00:28 ] @
[ petarm @ 20.12.2010. 10:25 ] @
[ Bojan Basic @ 24.12.2010. 19:51 ] @
Striktno gledano, ne možeš. Tačno je da se funkcija neko vreme približavala toj vrednosti, ali ko garantuje da neće početi da divlja tamo negde oko
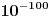 ? ?S druge strane, ako su ti ovo neki realni proračuni, i ako imaš nekog razloga za pretpostavku da se tvoja funkcija ponaša relativno „lepo“, onda cenim da vrednost koju tražiš zaista jeste oko 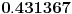 . U prilogu je račun s malo pojačanom preciznošću (što je omogućilo smanjivanje parametra . U prilogu je račun s malo pojačanom preciznošću (što je omogućilo smanjivanje parametra  ). ).[ petarm @ 04.01.2011. 13:26 ] @
[ Bojan Basic @ 20.01.2011. 20:38 ] @
Ne, ne možeš, ni približno.
Prvo — kad koristiš funkciju NSolve, moraš navesti po kojoj promenljivoj tražiš rešenje. (Ovo što si ti dobio je najpre gomila poruka o greškama, a potom je izračunata numerička vrednost koju integral treba da ima kako bi zadovoljio postavljenu jednačinu.) No, to svakako nije u tvom slučaju bitno, jer — drugo — NSolve radi samo za polinomne jednačine. Ako dobro razumem šta ti je bio cilj, onda pokušaj koristiti FindRoot. [ petarm @ 05.02.2011. 11:21 ] @
Imam problem u programu Mathematica sa funkcijom FindRoot. Nece da mi resi nesto sto bi moralo cini mi se? Prikacio sam dokument ovde
[ atomant @ 05.02.2011. 12:58 ] @
Ne mozes da koristis NIntegrate, jer u tom trenutku program ne zna sta je T2. NIntegrate vraca numericke, a ne simbolicke vrednosti.
[ petarm @ 05.02.2011. 13:45 ] @
Hvala na pomoci. Izbrisao sam N i pokusavam sa Integrate ispod FindRoot-a. Mathematica vec neko vreme radi. Vredi li da cekam?
[ petarm @ 05.02.2011. 14:32 ] @
Ne znam da li moze da resi. Mislim da nece moci. A da li je izvodljivo nekom transformacijom izraza izvuci ovaj clan sa T2 ispred integrala, a zatim raditi NIntegrate? Ovako odokativno mi ne pada nista na pamet. Mozda razvoj oko 0 pa onda videti sta se dobije?
[ atomant @ 05.02.2011. 14:33 ] @
Zaboravio sam da se ulogujem.
[ petarm @ 05.02.2011. 14:41 ] @
Ne moze se transformisati, a ni razviti u red. Neki nacin ipak mora postojati. Atomant imas neku ideju?
[ petarm @ 05.02.2011. 14:52 ] @
Nije vredelo cekati
[ SrdjanR271 @ 05.02.2011. 15:12 ] @
Mozda bi moglo da se razvije u tejlorov red f-je 3 promenljive.
Tu bi integrali bili laki, a dobio bi jednacinu po T2. Probaj da nadjes koeficijente u Mathematici, sam sastavi posle red. Ja sam probao Series[f-ja,{x,0,3},{y,0,3},{z,0,3}] i razvije ga a z ima negativne stepene mada mi je cudno kad je f(0,0,0) beskonacno ili nije? Probao sam u okolini tacke (1,1,1) i tu je ok razvoj Odradio sam trostruki integral i dobio j-nu po T2 Nasao sam sa FindRoot[] tacke, za nekoliko se dobija 0,42... Pretpostavljam da kad bi se uzelo vise clanova reda da bi bilo tacnije al to ti probaj Sta god dobijem za T2 daje 0,42 nikad blize nuli? [ SrdjanR271 @ 05.02.2011. 15:30 ] @
Sad sam radio razvoj u okolini Pi/2 do cetvrtih stepena
nasao T2=10220.3 mnogo blize nuli nego ranije dobija se 0.04... [ SrdjanR271 @ 05.02.2011. 15:41 ] @
Za T2=10877.151
dobijam 5.37233*10^-7 Za T2=10877.2 je manje od nule Tako da ti je tu izmedju jedna nula, Za T2=10877.159016701 rezultat je na -15 [Ovu poruku je menjao SrdjanR271 dana 05.02.2011. u 20:24 GMT+1] [ Panicarka @ 22.03.2012. 22:35 ] @
Moze li mi neko pomoci da resim sledeci problem?
Evo sta meni treba. Sve promenljive koje imam su pozitivne i vecina njih je izmedju 0 i 1. Dobijem neki duzi izraz recimo : a+b-2c-d^2 i tako dalje koji treba da bude uvek pozitivan (to meni treba). E sad, meni je potrebno da ga matematika prebaci u neki oblik koji je uvek pozitivan. Recimo (a-2b+c-d-e)^2 +4b^2c^2+p*(1-a)+a+b Znaci, potrebno mi je da matematika pronadje oblik koji je ekvivalentan mom izrazu, a koji predstavlja zbir tih promenljivih koje su pozitivne i kvadrata izraza koji sadrze predznak minus tako da na osnovu tog oblika moze da se zakljuci da je izraz uvek pozitivan. Evo jos jednog prostog primera da bude jasnije: Recimo izraz: x^2-2xy+y^2+4x+5y+4x^2-4x+1 matematika bi trebalo da prebaci u oblik (x-y)^2+(2x-1)^2+4x+5y koji predstavlja zbir dva kvadrata i dva broja koja su po uslovu pozitivna pa se moze zakljuciti da je izraz pozitivan dok se iz prvobitnog oblika to ne vidi. Unapred hvala expertima koji ce mi pomoci :) [ Nedeljko @ 23.03.2012. 16:03 ] @
Nemam pojma kako se koristi paket matematika, ali matematički gledano, radi se o problemu ekvivalentnom desetom Hilbertovom problemu.
Dokazano je da postoji polinom sa dve promenljive i realnim koeficijentima koji je nenegativan za sve realne vrednosti promenljivih, ali se ne može predstaviti kao konačan zbir kvadrata realnih polinoma. Međutim, svaka racionalna funkcija sa realnim koeficijentima koja je nenegativna za sve realne vrednosti promenljivih za koje je definisana (za neke realne vrednosti promenljivih može biti nedefinisana) može se predstaviti kao konačna suma kvadrata racionalnih funkcija. Dakle, u opštem slučaju se nenegativan realan polinom može predstaviti kao konačan zbir kvadrata realnih racionalnih funkcija. Najpre treba prebaciti problem u ekvivalentan oblik u kome se ne pojavljuju ograničenja promenljivih. Primera radi, ako imamo ograničenje da je 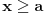 , onda treba uvesti smenu , onda treba uvesti smenu 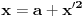 . .Ograničenje 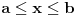 se uklanja smenom se uklanja smenom 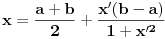 . .Ograničenje 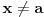 se uklanja smenom se uklanja smenom 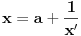 . .Kada se uklone sva ograničenja, onda je moguće primeniti neki od algoritama za rešavanje desetog Hilbertovog problema. [Ovu poruku je menjao Nedeljko dana 23.03.2012. u 18:53 GMT+1] [ Panicarka @ 24.03.2012. 09:16 ] @
Hvala puno na odgovoru. Sada sam pogledala. Mathematica nema algoritam za resavanje Hilbertovog problema. Pomocu kog programa da primenim taj algoritam?
[ Panicarka @ 24.03.2012. 09:20 ] @
Po kom principu se uvode ova ogranicenja? Kako se dobijaju ove formule?
[ Nedeljko @ 24.03.2012. 10:10 ] @
Nemam pojma koji softver rešava deseti Hilbertov problem.
Što se ograničenja tiče, hajde razmisli, šta je skup vrednosti funkcije 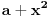 kada kada  ide preko svih realnih brojeva? Šta je skup vrednosti funkcije ide preko svih realnih brojeva? Šta je skup vrednosti funkcije  ? To je odsečak ? To je odsečak  . Šta je skup vrednosti funkcije . Šta je skup vrednosti funkcije  kada kada  ide preko celog domena te funkcije? ide preko celog domena te funkcije?Ako bih imao ograničenje  najpre bih uveo smenu najpre bih uveo smenu 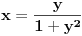 uz novo ograničenje uz novo ograničenje 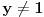 , a onda bih uveo smenu , a onda bih uveo smenu 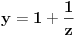 . .Da li sada možeš da izvedeš formule za 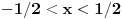 ? ?[ Nedeljko @ 24.03.2012. 14:29 ] @
Izvinjavam se, ne radi se o desetom, već o sedamnastom Hilbertovom problemu.
[ Nedeljko @ 24.03.2012. 15:39 ] @
E, da, ako su polinomi do drugog stepena, onda postoji jednostavnije rešenje.
[ Panicarka @ 25.03.2012. 13:39 ] @
Polinom sadrzi 5 promenljivih od kojih su 4 u intervalu (0,1), a jedna je veca od nule. Najvisi stepen je 2.
[ Panicarka @ 25.03.2012. 14:03 ] @
Poklapa se delimicno sa 17. Hilbertovim problemom s tim sto ne moraju svi clanovi da budu kvadrati. Neki mogu da budu oblika a*(1-b)*c^2 recimo, zbog uslova da je b na primer izmedju 0 i 1, a>0.
[ Nedeljko @ 25.03.2012. 17:20 ] @
Citat: Panicarka: Polinom sadrzi 5 promenljivih od kojih su 4 u intervalu (0,1), a jedna je veca od nule. Najvisi stepen je 2. Pa, daj napiši jednačinu. Citat: Panicarka: Poklapa se delimicno sa 17. Hilbertovim problemom s tim sto ne moraju svi clanovi da budu kvadrati. Neki mogu da budu oblika a*(1-b)*c^2 recimo, zbog uslova da je b na primer izmedju 0 i 1, a>0. Sedamnaesti Hilbertov problem rešava i ovo što ti treba, jer je oblik u vidu zbira kvadrata tebi dovoljno dobar. Koliko shvatam, član navedenog oblika ne mora da se pojavljuje. [ Panicarka @ 25.03.2012. 23:47 ] @
Citat: Nedeljko: Sedamnaesti Hilbertov problem rešava i ovo što ti treba, jer je oblik u vidu zbira kvadrata tebi dovoljno dobar. Koliko shvatam, član navedenog oblika ne mora da se pojavljuje. Tacno tako. Ja sam samo napisala da ne moraju da budu kvadrati da bi izraz bio pozitivan. Ali zbir kvadrata svakako resava problem. [ Ana997 @ 20.10.2012. 13:32 ] @
Bila bih vrlo zahvalna ako bi mi neko mogao pomoći oko nekih zadataka iz matematike :/ s tim predmetom imam poteškoća oduvek :'(
Naime, nikako ne mogu da shvatim rastavljanje polinoma na činioce. Uprkos tome što znam one formule.Ako bi neko mogao da mi kaže neki princip po kome se radi, ili neke zakonitosti. Imam užasnu baba - profesorku koja nošta ne ume. :'( Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|