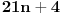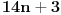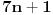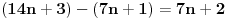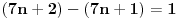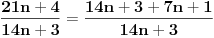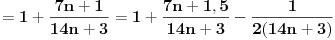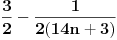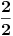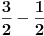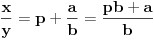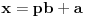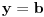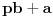[ petarm @ 18.12.2010. 16:00 ] @
|
[ Nedeljko @ 18.12.2010. 16:55 ] @
[ Fermion @ 18.12.2010. 18:18 ] @
[ Nedeljko @ 20.12.2010. 09:19 ] @
[ Fermion @ 20.12.2010. 10:18 ] @
Možda sam i pogrešio, ali vaš kontraprimer ne odgovara uslovu zadatka. Pošto je n prirodan broj razlomak
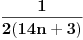 ne može imati vrednost ne može imati vrednost 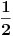 . .Po mojoj proceni: Neka su 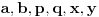 prirodni brojevi i neka važi prirodni brojevi i neka važi 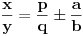 tada pod uslovom da je tada pod uslovom da je 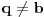 i i 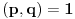 , tj. brojevi p i q su uzajamno prosti, razlomak , tj. brojevi p i q su uzajamno prosti, razlomak 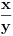 nije skrativ ako i samo ako su brojevi a i b uzajamno prosti, tj. ako razlomak nije skrativ ako i samo ako su brojevi a i b uzajamno prosti, tj. ako razlomak 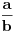 nije skrativ. nije skrativ.Ne bih trenutno znao da to dokažem, ali mi intuitivno deluje tačno, to mi je ideja u ovom rešenju. Mada opet kažem, možda sam i pogrešio. [ Nedeljko @ 20.12.2010. 10:48 ] @
Citat: Fermion: Po mojoj proceni: Neka su 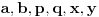 prirodni brojevi i neka važi prirodni brojevi i neka važi 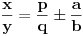 tada pod uslovom da je tada pod uslovom da je 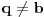 i i 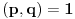 , tj. brojevi p i q su uzajamno prosti, razlomak , tj. brojevi p i q su uzajamno prosti, razlomak 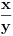 nije skrativ ako i samo ako su brojevi a i b uzajamno prosti, tj. ako razlomak nije skrativ ako i samo ako su brojevi a i b uzajamno prosti, tj. ako razlomak 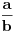 nije skrativ. nije skrativ.Pa, evo, 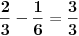 . .Tvoja ideja bi se mogla sprovesti ovako: Obzirom da 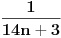 nije skrativ, nije ni nije skrativ, nije ni 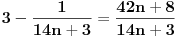 . No, onda je razlomak . No, onda je razlomak 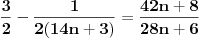 eventualno skrativ sa eventualno skrativ sa  , što i jeste slučaj. No, to znači da je razlomak , što i jeste slučaj. No, to znači da je razlomak 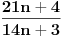 dobijen skraćivanjem sa dobijen skraćivanjem sa  neskrativ. neskrativ.[ Fermion @ 20.12.2010. 11:33 ] @
Citat: Nedeljko: Pa, evo, 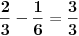 . .Tvoja ideja bi se mogla sprovesti ovako: Obzirom da 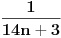 nije skrativ, nije ni nije skrativ, nije ni 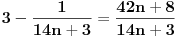 . No, onda je razlomak . No, onda je razlomak 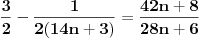 eventualno skrativ sa eventualno skrativ sa  , što i jeste slučaj. No, to znači da je razlomak , što i jeste slučaj. No, to znači da je razlomak 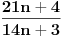 dobijen skraćivanjem sa dobijen skraćivanjem sa  neskrativ. neskrativ.Odnosno: 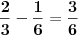 Znači li to da važi sledeće: Neka su 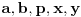 prirodni brojevi i neka važi prirodni brojevi i neka važi 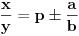 tada pod uslovom da tada pod uslovom da 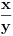 nije skrativ ako i samo ako su brojevi a i b uzajamno prosti, tj. ako razlomak nije skrativ ako i samo ako su brojevi a i b uzajamno prosti, tj. ako razlomak 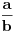 nije skrativ. nije skrativ.Pitam zbog ovog koraka u vašoj zadnoj poruci: Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|