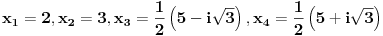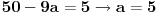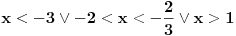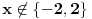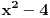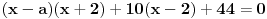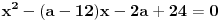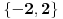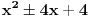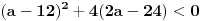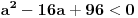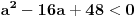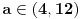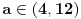[ Lucass @ 20.12.2010. 21:20 ] @
 Ovo se resava preko t...  Ako ova funkcija sadrzi tacku A(3,5)  Ovde treba da se nadje za koje vrednosti parametra a izraz nema realna resenja... to je D < 0 D= b^2 - 4ac  Samo da se resi... Zadaci su sa pismenog iz kvadratnih nejednacina i kvadratne funkcije... Krajnje lako, uradio sam sve, ali moram da isproveravam Ako nekog ne mrzi da uradi... Bilo koji I da, meni nisu potrebni postupci, dovoljna su mi resenja [Ovu poruku je menjao Lucass dana 20.12.2010. u 22:31 GMT+1] |