[ edisnp @ 24.12.2010. 21:01 ] @
| Zadatak je sledeci Neka je n ∈ N. Dokazati da je broj n(n − 3)(n^2- 3n + 14) deljiv sa 8. kad se ovo izmnozi dobije se n^4-6n^3+23n^2-42n kako dalje da nastavim |
|
[ edisnp @ 24.12.2010. 21:01 ] @
[ Janinka @ 24.12.2010. 21:14 ] @
Da pokusas pomocu matematicke indukcije?
[ Fermion @ 24.12.2010. 21:30 ] @
Može ovo jednostavno da se reši bez tolikog množenja i matematičke indukcije.
Primetimo da je polazni izraz ekvialentan sa: 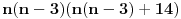 Uvedimo smenu: 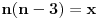 Izraz postaje 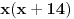 Pošto su brojevi n i n-3 različite parnosti, njihov proizvod je paran broj, pa je x parno. Ako je x deljivo sa 4 broj x+14 je takođe paran, a proizvod ta dva broja je deljiv sa 8. Ako x nije deljivo sa 4 broj x+14 mora biti deljiv sa četiri 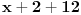 (jer bar jedan od dva uzastopna parna broja mora biti deljiv sa 4). (jer bar jedan od dva uzastopna parna broja mora biti deljiv sa 4).Prema tome i x i x+14 su parni brojevi za svako n iz skupa prirodnih brojeva, i jedan od ta dva je deljiv sa 4. Prema tome njihov proizvod je deljiv sa 8, čime je tvrđenje dokazano. [ Fermion @ 24.12.2010. 21:48 ] @
Evo još jednog rešenja.
Neka je n paran broj. Tada ga možemo pisati u obliku n=2k, gde je k prirodan broj. Ako to stavimo u polazni izraz: 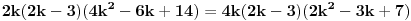 Ako je k parno ovo je jasno deljivo sa 8. Ako je k neparno onda je 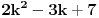 parno, pa je i u ovom slučaju polazni izraz deljiv sa 8. parno, pa je i u ovom slučaju polazni izraz deljiv sa 8.Neka je n neparan broj. Tada ga možemo pisati u obliku n=2k+1. Ako se to stavi u polazni izraz: 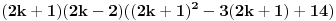 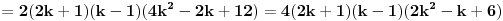 Ako je k parno onda je 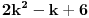 parno, čime je dokazano da je polazni oblik deljiv sa 8. parno, čime je dokazano da je polazni oblik deljiv sa 8.Ako je k neparno onda je k-1 parno, pa je i u ovom slučaju polazni oblik deljiv sa 8. Prema tome za svaki prirodan broj n važi da je 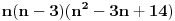 deljivo sa 8. deljivo sa 8.[ Nedeljko @ 24.12.2010. 22:08 ] @
Sjajno rešenje. Ipak, uvek treba znati standardna rešenja, kao što je induktivno.
Dakle, za 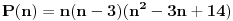 se lako proverava da je se lako proverava da je 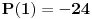 , što je deljivo sa , što je deljivo sa  . Dalje je . Dalje je 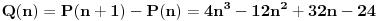 . Ako dokažemo da je . Ako dokažemo da je 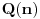 deljivo sa deljivo sa  , onda tvrđenje sledi indukcijom. , onda tvrđenje sledi indukcijom.Deljivost 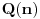 sa sa  dokazujemo istom metodologijom. dokazujemo istom metodologijom. 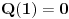 . Dovoljno je dokazati da je . Dovoljno je dokazati da je 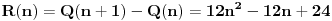 deljivo sa deljivo sa  . .Konačno, indukcijom dobijamo da je to ispunjeno zbog 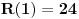 i i 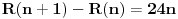 . .Ovakva metodologija pali uvek. Iz ovog dokaza sledi čak i deljivost sa 24. [ Fermion @ 24.12.2010. 22:53 ] @
Deljivost sa 24 bi se mogla dokazati i nekim od gornjih rešenja, ako se dodatno dokaže deljivost sa 3.
Primetimo da je jedan od brojeva n, n-1 i n+1 deljiv sa 3. Ako je n deljivo sa 3 tvrđenje je očigledno. Ako je n-1 deljivo sa 3: 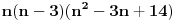 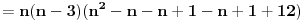 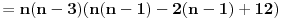 Preostaje da se ispita slučaj kada je n+1 deljivo sa 3: 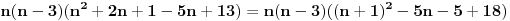 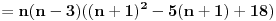 Prema tome za svaki prirodan broj n važi da je 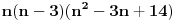 deljivo sa 24. deljivo sa 24.[ petarm @ 24.12.2010. 23:18 ] @
Htegoh samo edisnp-u da skrenem paznju na jednu stvar. Uvek se trudi kod ovakvih zadataka da rastavis neki polinom na cinioce, a ne kada dobijes rastavljen da mnozis. Ili npr. neki proizvod + neki broj koji deli to sto trebas da proveris.
Dakle ako hoces da dokazes da je broj 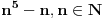 deljiv sa 30, rastavi ovo na proizvod prostih cinilaca deljiv sa 30, rastavi ovo na proizvod prostih cinilaca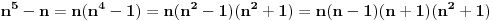 pa ispituj. Ovaj drugi slucaj mi je teze da iskonstruisem. Al ideja je ova hoces da dokazes da je neki 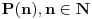 deljiv sa 33. Onda ovo mozda mozes da zapises npr. kao deljiv sa 33. Onda ovo mozda mozes da zapises npr. kao 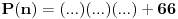 :D i da dokazes da je 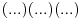 deljiv sa deljiv sa 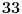 . A dokaz za . A dokaz za 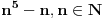 bi mogao sam da izvedes pa i napises ovde zasto da ne! bi mogao sam da izvedes pa i napises ovde zasto da ne! [Ovu poruku je menjao petarm dana 25.12.2010. u 01:33 GMT+1] [ edisnp @ 25.12.2010. 00:50 ] @
Mislim da je ovako n^5-n mozemo da napisemo
kao:n(n-1)(n+1)(n-2)(n+2)+5n(n+1)(n-1) dalje matematickom indukcijom za n=1 dobije se 0 sto je deljivo sa 30, za n=k dobijamo pretpostavku k(k-1)(k+1)(k-2)(k+2)+5k(k+1)(k-1) za n=k+1 se dobija (k+1)(k)(k+2)(k^2+2k+2). 5k(k+1)(k-1) je deljivo sa 5 i 10 zbog cinioca 5 posto je deljivo sa 10 onda je i sa 30 ne znam koliko sam blizu pokusao sam matematickom indukcijom da dodjem do nekog resenja. [ Fermion @ 25.12.2010. 07:51 ] @
S obzirom da je:
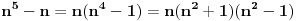 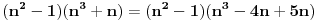 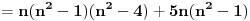 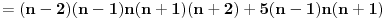 Pošto su n-2, n-1, n, n+1 i n+2 uzastopni prirodni brojevi bar jedan od njih je deljiv sa 5. Proizvod 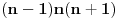 je proizvod tri uzastopna broja, od kojih je jedan deljiv sa tri i bar jedan deljiv sa 2, pa je pomenuti proizvod deljiv sa 6. Pošto je je proizvod tri uzastopna broja, od kojih je jedan deljiv sa tri i bar jedan deljiv sa 2, pa je pomenuti proizvod deljiv sa 6. Pošto je 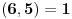 sledi da je sledi da je 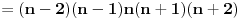 deljivo sa 30. deljivo sa 30. Drugi sabirak je deljiv sa 6, jer je 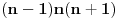 deljivo sa 6, a zbog koeficijenta 5 ceo ovaj deo deljiv sa 30. deljivo sa 6, a zbog koeficijenta 5 ceo ovaj deo deljiv sa 30.Odavde sledi da je 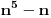 deljivo za svako n, gde deljivo za svako n, gde 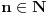 . .[ Nedeljko @ 25.12.2010. 08:09 ] @
Pa, već sam ti dao opšti postupak koji uvek pali.
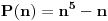 . Da bismo indukcijom dokazali da je . Da bismo indukcijom dokazali da je 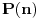 deljivo sa deljivo sa 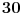 , treba dokazati da je , treba dokazati da je 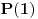 deljivo sa deljivo sa 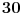 i da je i da je 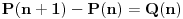 deljivo sa deljivo sa 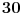 . . 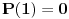 i i 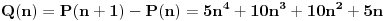 . .Da bismo indukcijom dokazali da je 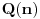 deljivo sa deljivo sa 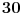 , treba dokazati da je , treba dokazati da je 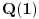 deljivo sa deljivo sa 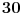 i da je i da je 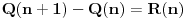 deljivo sa deljivo sa 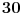 . . 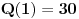 i i 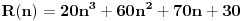 . .Da bismo indukcijom dokazali da je 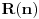 deljivo sa deljivo sa 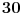 , treba dokazati da je , treba dokazati da je 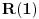 deljivo sa deljivo sa 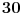 i da je i da je 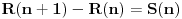 deljivo sa deljivo sa 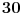 . . 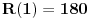 i i 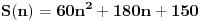 . .Kraj. [ Fermion @ 25.12.2010. 08:36 ] @
Evo i rešenja sa matematičkom indukcjom:
1)Za n=1 je 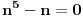 , što je deljivo sa 30. , što je deljivo sa 30.2)Pretpostavimo da je za n=k ispunjen uslov zadatka: 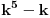 je deljivo sa 30 je deljivo sa 303) Treba dokazati da je za 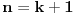 važi da je važi da je 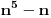 deljivo sa 30. deljivo sa 30.Ako je 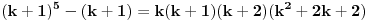 deljivo sa 30, onda je i: deljivo sa 30, onda je i: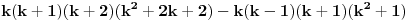 deljivo sa 30. deljivo sa 30.Ovo je ekvivalentno sa uslovom da je 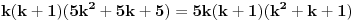 deljivo sa 30. deljivo sa 30.Pošto je: 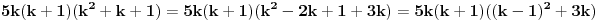 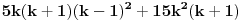 . .Pošto je proizvod 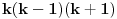 deljiv sa 6, sledi da je prvi sabirak deljiv sa 30, dok za drugi to jasno važi pošto jedan od brojeva k i k+1 mora biti paran. deljiv sa 6, sledi da je prvi sabirak deljiv sa 30, dok za drugi to jasno važi pošto jedan od brojeva k i k+1 mora biti paran.Time je pokazano da je za svako n 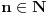 važi da je 30 delilac važi da je 30 delilac 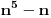 . .[ Fermion @ 25.12.2010. 08:47 ] @
@Nedeljko
Dadoh nešto drugačije rešenje matematičkom indukcijom. Moram priznati da je vaš postupak sa matematičkom indukcijom opštiji, pa zato i praktičniji. Ipak ja težim ovakve zadatke da rešavam bez pozivanja na nju, jer teorija brojeva nudi mnogo drugih načina pored ovog da se na originalan način reši zadatak. Ali ako ne možemo pronaći drugo rešenje svakako je najbolje koristiti matematičku indukciju. Bar ja tako mislim. [ petarm @ 25.12.2010. 09:27 ] @
Citat: Fermion: S obzirom da je: 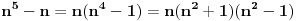 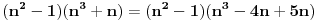 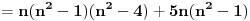 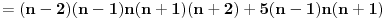 Pošto su n-2, n-1, n, n+1 i n+2 uzastopni prirodni brojevi bar jedan od njih je deljiv sa 5. Proizvod 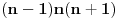 je proizvod tri uzastopna broja, od kojih je jedan deljiv sa tri i bar jedan deljiv sa 2, pa je pomenuti proizvod deljiv sa 6. Pošto je je proizvod tri uzastopna broja, od kojih je jedan deljiv sa tri i bar jedan deljiv sa 2, pa je pomenuti proizvod deljiv sa 6. Pošto je 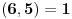 sledi da je sledi da je 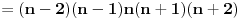 deljivo sa 30. deljivo sa 30. Drugi sabirak je deljiv sa 6, jer je 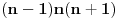 deljivo sa 6, a zbog koeficijenta 5 ceo ovaj deo deljiv sa 30. deljivo sa 6, a zbog koeficijenta 5 ceo ovaj deo deljiv sa 30.Odavde sledi da je 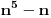 deljivo za svako n, gde deljivo za svako n, gde 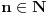 . .I odavde je pogodno 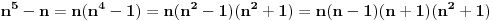 Ako nijedan od brojeva 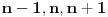 nije deljiv sa 5, onda je nije deljiv sa 5, onda je  oblika oblika 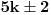 . Pa zamenim to u . Pa zamenim to u 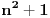 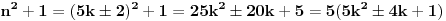 I to je to prakticno! Posto imamo proizvod 3 uzastopna prirodna broja deljivost sa 6 je ocigledna! [ Fermion @ 25.12.2010. 10:14 ] @
Evo još jednog rešenja.
Ako je n paran, tada je i 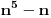 parno. Ako je n neparno tada je opet parno. Ako je n neparno tada je opet 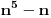 kao razlika neparnih brojeva paran broj, što dokazuje deljivost sa 2. kao razlika neparnih brojeva paran broj, što dokazuje deljivost sa 2.Broj n je kongruentan ili -1 ili 0 ili 1 po modulu 3. Pošto u prvom slučaju 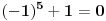 , u drugom se opet dobija nula, u trecem: , u drugom se opet dobija nula, u trecem: 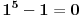 sledi da je broj sledi da je broj 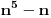 deljiv sa 3. deljiv sa 3.Po modulu 5 broj n je kongruentan nekom od brojeva -2,-1,0,1,2. U prvom slučaju 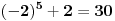 , za 1,-1, 0 je kao i u dokazu za 3, dok je , za 1,-1, 0 je kao i u dokazu za 3, dok je 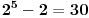 , pa je broj deljiv i sa 5. , pa je broj deljiv i sa 5.Sledi da je broj 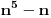 deljiv sa 30. deljiv sa 30.[ Nedeljko @ 25.12.2010. 10:56 ] @
@edinsp
Pusti ovu dvojicu koji iznose neka elegantnija rešenja, koja funkcionišu u specijalnim slučajevima i zahtevaju cake. Samo te zbunjuju. Nauči ti opšte šablonsko rešenje koje sam ti dao, pa kada tu budeš siguran, onda možeš da se igraš sa cakama. [ petarm @ 25.12.2010. 11:39 ] @
Ne znam koje je edisnp godiste? Ako je npr. 1. razred srednje tesko da zna binomni obrazac. [ edisnp @ 25.12.2010. 11:43 ] @
prvi sam razred matematickog smera tj 1995 godiste
[ Nedeljko @ 25.12.2010. 12:08 ] @
Koliko vidim, zna da izmnoži polinome.
[ petarm @ 25.12.2010. 12:52 ] @
[ edisnp @ 25.12.2010. 13:21 ] @
Ok primljeno k znaju za ubuduce
[ Sini82 @ 25.12.2010. 14:02 ] @
U prvom razredu matematičke gimnazije ne radi se matematička indukcija i za očekivati je od učenika da riješe ovaj zadatak primjenom znanja koja imaju iz teorije brojeva.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|